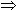 a|(bx + cy) for all integers x,y
a|(bx + cy) for all integers x,y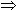 a|(bx + cy) for all integers x,y Let a be a nonnegative integer and let b be a positive integer. Then there exist natural numbers q and t such that
a|(bx + cy) for all integers x,y Let a be a nonnegative integer and let b be a positive integer. Then there exist natural numbers q and t such that | Back | Table of Contents |
|
|
CongruencesIn this section we will introduce two algebraic systems which can be constructed from integers. These systems will provide us with enlightening examples of many algebraic phenomena and will prove to be important in their own right. Throughout this section let n be a positive integer.
Definition 1: Let
Example 1:
If n is clear from context, we will sometimes write
Proposition 2: (1) For all
(2) If
(3) If
If Proof: (1),(2) - Clear.
(3) If
(4) If
n|(a + c) - (b + d)
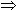 (a + c) (a + c)  (b + d)(mod n). (b + d)(mod n).
Also, we have
ac
 bc(mod n), bc bc(mod n), bc  bd(mod n). bd(mod n).
Therefore by part (3), we have
ac
 bd(mod n). bd(mod n).
Many facts concerning congruences are quite old. For example, in the beginning of the seventeenth century, the jurist and amateur mathematician Fermat
proved that if a is an integer and p is a prime such that
anxn + an-1xn-1 + ... + a0
 0(mod m), 0(mod m),
where m,a0,...,an are given integers and x is to be determined. The problem as stated is incredibly difficult and much nineteenth century research in number theory was aimed at its solution, which is not complete today. Just to get a feel for Gauss's work, let us consider the particular congruence
x2
 a(mod p) a(mod p)
where a is a given integer and p is a prime. The congruence may or may not have a solution x. For example, if
One of Gauss's greatest achievements is the law of quadratic reciprocity, which asserts that if p and q are distinct, odd primes, then
(p/q)(q/p) = (-1)(p-1)(q-1)/4,
(2/p) = (-1)(p2-1)/8,
(-1/p) = (-1)(p-1)/2.
Using the quadratic reciprocity law, it is possible to determine precisely when the congruence Much work on congruences of higher degree was undertaken during the nineteenth century and these investigations have led to some of the most significant developments of the twentieth century and are still objects of research. In this section we will concentrate on the theory of linear congruences. If k is an arbitrary integer, let k denote the set of all integers congruent to k modulo n. Then
Then sets k are called residue classes modulo n. Suppose that k is a given residue class. The division algorithm says that there exist we see that k is the same as one of the residue classes
0,1,...,n-1.
Note that none of these latter residue classes are equal. For if
so that
0,1,2...,n-1.
Let us denote the set of all residue classes modulo n by Zn. From our above discussion, it is clear that every integer is contained in some residue class modulo n, and therefore
Moreover, no integer is contained in two of the residue classes
i
 j = j = 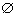
Let us define addition and multiplication of elements of Zn as follows:
a + b = a + b,
a · b = a · b.
That is, the sum (respectively, product) of two residue classes a and b is the residue class containing
a
 c(mod n), b c(mod n), b  d(mod n), d(mod n),
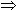 (a + b) (a + b)  (c + d)(mod n), (c + d)(mod n),
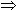 a + b = c + d. a + b = c + d.
Therefore, the operation of addition of residue classes is consistent. A similar argument holds for multiplication. Addition and multiplication are commutative and associative and the two operations obey the distributive law
a·(b + c) = a·b +
a·c.
The residue class 0 is the identity element with respect to addition: The residue class 1 is the identity element with respect to multiplication:
Every residue class a has an inverse -a with respect to addition. In fact we may set
a + -a = -a + a = 0.
Thus, in most respects, the algebraic system Zn possesses the same properties as Z. However, there is at least one important difference. Recall that we proved
that the product of two nonzero integers is nonzero. This property of Z does not carry over to Zn. For example, let us consider Z6. We clearly
have
3 · 2 = 6 = 0.
In this circumstance we say that 3 and 2 are divisors of zero. We leave to the reader the verification of the fact that if n is prime, then Zn has no divisors of zero, while if n > 1 and not prime, then Zn always has divisors of zero.
Note that if
Example 2:
Since  (6) = 2, (6) = 2,  (7) = 6, (7) = 6,  (10) = 4. (10) = 4.
The function If 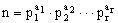
is the decomposition of n into a product of powers of distinct primes, then (1)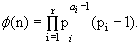
The reader should verify that this formula works in the special cases of the examples given above.
Proposition 3: Suppose that
Proof: Since
By Proposition 3, · defines a law of multiplication among reduced residue classes. Since 1
Let
a · b = b · a = 1.
That is, a has an inverse with respect to multiplication.
Proof: It suffices to find
a · b
 1 (mod n). 1 (mod n).
Since
a · x + n · y = 1.
We clearly have
a · x
 1(mod n). 1(mod n).
Therefore, we may set
Proposition 4 has an interesting application. Let
ax + by = c
in integers. Such an equation is called a Diophantine equation, after the Greek mathematician Diophantus, who first studied its solutions. If
a'x + b'y = c'.
But
ax
 c(mod b). c(mod b).
In turn, the congruence (3) is equivalent to the equation (4)
a · x = c
among residue classes of Zb. By Proposition 4, since
a* · a · x = a* ·
c
 x = a* · c. x = a* · c.
Therefore, in order to solve Equation (2), it is sufficient to choose x so that
x
 a*c(mod b). a*c(mod b).
Then Let us now give an example to show that this whole process is computationally viable. Consider the equation
3x + 5y = 12
Then
x
 24 (mod 5), 24 (mod 5),
which is equivalent to (5)
x
 4 (mod 5). 4 (mod 5).
For given x satisfying (5), set
y = (-3x + 12)/5.
For example, some solutions are |
| Back | Table of Contents |