Number Theory in Z
In this section we will study some of the arithmetic properties of integers. The properties which we establish will motivate many of the abstract notions which we will consider later.
We will say that a|b (read "a divides b") if
(1)
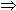 a|c,
a|c,
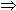 a|(bx + cy) for all integers x,y
a|(bx + cy) for all integers x,y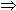 b = a or b = -a.
b = a or b = -a.We will leave proofs of (1) and (2) to the reader. To prove (3), let us prove two auxiliary assertions
(3a)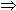 a|(b + c),
a|(b + c),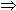 a|bx for all x.
a|bx for all x.
Assertions (3a) and (3b) imply (3) since if a|b, a|c, then a|bx, a|cy by (3b), which implies that a|(bx + cy) by (3a). To prove (3a), notice that if a|b, a|c, there exists k and m such that
Let us now prove (4). If a|b then ±a|±b, so that is suffices to consider the case where
We say that c is a greatest common divisor of a and b, provided that.
1. c > 0.
2. c|a, c|b.
3. Whenever d is an integer such that d|a, d|b, then d|c.
Property (2) asserts that c is a divisor of both a and b, that is, a common divisor of a and b. Property (3) asserts that among all common divisors of a and b, c is the "greatest" in the sense that every common divisor of a and b is also a divisor of c. We denote c by
Exercise 1: Suppose that a and b have a greatest common divisor c. Show that c is the largest denominator of a and b.
It is not obvious that two integers have a greatest common divisor. Nor is it obvious that two integers have only one greatest common divisor. Let us clarify the second point: If a greatest common divisor exists, it must be unique. For suppose that c1 and c2 both satisfy (1)-(3). Then by (2), c2|a, c2|b. Thus by (3) for c1, we see that c2|c1. Similarly, c1|c2. Therefore by (4)
Proposition 1: Suppose that a and b are not zero. Then a and b have a greatest common divisor.
Proof: We noted that the proposition is not at all obvious. In order to prove it, a tremendously ingenious idea is required. Let
 Z}
Z}
We will prove that S contains the common divisor of a and b. If
 S,
S, S.
S. S
S S
S S | z > 0}.
S | z > 0}. S,
S,
(5)
Therefore, if d|a, d|b, we see that d|c by (3). Thus, properties (1) and (3) hold. In order to prove (2), let us prove the following.
Claim: Each element of S is a multiple of c.
It clearly suffices to show that every positive element of S is a multiple of c. Therefore, let  S+.
S+.
By equation (5) we see that
which implies that r  S. If
S. If  S+,
S+,
In order to complete the proof of the proposition, we note that since  S,
S, S,
S,
Corollary 2: Let a and b be integers, at least one of which is nonzero, and let c be the greatest common divisor of a and b. Then there exist integers x and y such that.
We say that two nonzero numbers are relatively prime if their greatest common divisor is 1. By the preceding corollary, we immediately derive
If a and b are relatively prime, then there exist integers x and y such that ax + by = 1.Corollary 3: If a and b are relatively prime, then there exist integers x and y such that
Henceforth, we will denote by
Definition 4: A prime number is a natural number
For example, 2 and 3 are primes, but
Let n be an integer greater than 1. Then n can be expressed as a product of primes. Lemma 5: Let n be an integer greater than 1. Then n can be expressed as a product of primes.
Proof: Let us reason by induction on n. The assertion is clearly true for
As a simple application of the lemma, we can prove
Theorem 6(Euclid): There exist infinitely many primes.
Proof: Let us reason by contradiction. Suppose that
is greater than 1, and is therefore divisible by some prime, by Lemma 5. But M is not divisible by any one of p1,...,pN. Thus there must exist a prime different from p1,...,pN, and a contradiction is reached.
There is a simple way of constructing a table of the primes, first discovered by the Greek mathematician Eratosthenes. Write down all of the natural numbers, beginning with 1:
Cross out all of the numbers divisible by 2, except for the first one, 2, to get
Next, cross out all of the multiples of 3, except for the first one to get
Four and its multiples have already been crossed out, so next cross out the multiples of 5, except for the first, and continue in this way. The natural numbers remaining will be precisely the primes and 1. For am additional example click on sieve example.
Lemma 5 asserts that every every nonzero integer can be expressed as a product of primes. Our last major result in this section will be to show that this expression is unique, that is, unique except for the arrangements of the factors. This fact is known as the fundamental theorem of arithmetic.
The notion of a prime was already known to the Greeks. In fact the fundamental theorem of arithmetic had its origins in Greek mathematics. The proof that there are infinitely many primes was known to Euclid, who included a proof in his Elements. If one looks at a table of primes, one of the interesting features which one notices is the rather irregular way in which the primes are distributed. For example, the primes below 100 are
in 1798 Legendre made some highly significant empirical investigations concerning the distributions of primes. For  (x)
(x) (x)
(x)
where A and B are numerical constants, not depending on x. By "approximately" Legendre meant that as x tends to infinity, the ratio
 (x)
(x)
tends to 1. Actually, Legendre did not know that
Gauss had done the same empirical experiments in 1792 and in 1793 without publishing them. Legendre was quite specific. He conjectured that
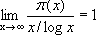
Statement (6) is called the prime number theorem.
The first substantial progress toward a proof of (6) was made by the Russian mathematician Tchebycheff in 1851-1852. He showed, among other things, that for all sufficiently large x,
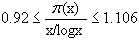
However, Tchebycheff's ideas could not be pushed far enough to prove the prime number theorem.
The year 1860 was the turning point in the efforts to give a proof of the prime number theorem. In that year Riemann published a paper in which he connected the function  (x)
(x) (x).
(x). (x)
(x)
Although Riemann was not able to prove the prime number theorem, his ideas figured prominently in the first proof, which was discovered independently by Hadamard and de la Vallee Poussin, both in 1896.
Let us now turn to the fundamental theorem of arithmetic. Before we are able to give a proof of this basic result, we must first establish two preliminary facts which are important in their own right. Again the ideas are Euclid's.
Lemma 7: Let a,b, and c be nonzero. If a divides bc and a and b are relatively prime, then a divides c.
Proof:By Corollary 3 there exist x and y such that
 acx + kay = c,
acx + kay = c,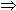 a(cx + ky) = c,
a(cx + ky) = c,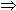 a|c.
a|c.Theorem 8 (Euclid): Let p be a prime. If p divides a product ab, then either p divides a or p divides b.
Proof: The result is clear if a or b is zero. Therefore, assume both a and b are nonzero. Assume that p does not divide a (denoted p a). Then since p is prime, a and p are relatively prime. There for, by Lemma 7, p|b.
a). Then since p is prime, a and p are relatively prime. There for, by Lemma 7, p|b.
The reader should have no difficulty showing that if  a,
a, b
b
A useful consequence of Theorem 8 is
Let p be a prime. If p divides
Corollary 9: Let p be a prime. If p divides
Proof:Follows by induction from theorem 8.
Let us now address ourselves to the fundamental theorem.
Theorem 10 (Fundamental Theorem of Arithmetic): Let n be an integer greater than 1. Then n can be represented as a product of primes
Moreover, the representation of n is unique up to the rearrangement of the factors. That is, if
Proof: The first assertion is true by Lemma 5. Let us proceed by induction on r. If
which implies that
(7)
By our induction assumption and equation (7), we see that