Pafnuty Lvovich Tchebycheff

In 1847 Pafnuty Tchebycheff was appointed to the University of St Petersburg. He became a foreign associate of the Institut de France in 1874 and also of the Royal Society.

His work on prime numbers included the determination of the number of primes not exceeding a given number. He wrote an important book Teoria sravneny on the theory of congruences in 1849.

In 1845 Bertrand conjectured that there was always at least one prime between n and 2n. Tchebycheff proved Bertrand's conjecture in 1850. Tchebycheff also came close to proving the prime number theorem, proving that if

((n)log n)/n

had a limit as n 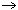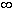then that limit is 1. He was unable to prove, however, that

lim ((n)log n)/n as n

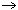
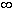
exists. The proof of this result was only completed two years after Tchebycheff's death by Hadamard and (independently) de la Vallée Poussin.

In his work on integrals he generalized the beta function and examined integrals of the form

x^p (1 - x)^q dx.

Tchebycheff was also interested in mechanics and studied the problems involved in converting rotary motion into rectilinear motion by mechanical coupling. The Tchebycheff parallel motion is three linked bars approximating rectilinear motion.

He wrote about many subjects, including probability theory, quadratic forms, orthogonal functions, the theory of integrals, the construction of maps, and the calculation of geometric volumes.