The Integers
One of the most important sets in all of mathematics is the set Z of integers:
In spite of centuries of effort by the greatest mathematical minds, there are many simple problems concerning Z which cannot be settled at the present time. For example, consider the problem of Fermat which was mentioned in historical perspectives, concerning the nonexistence of nonzero solutions of the equation
It is possible to construct the integers in terms of sets and to verify all the basic properties from the properties of sets. However, this is a rather drawn-out process, and would take us far afield from our central area of interest, so we will resist the temptation to provide a complete development of the integers.
The Basic Properties of Z
In the following discussion, we will present five basic sets of properties of the integers. Mathematicians have distilled these properties of the integers during centuries of investigations. The properties which we will assume have two convenient features: They agree with our preconceived notions about the integers and they form a natural point of departure for the development of less elementary properties.
On the set of integers, there are defined two binary operations, one called addition (denoted +) and one called multiplication (denoted ·). Our first three sets of properties of the integers are just some familiar properties of + and · .
I. Properties of Addition
A1. Associativity: If  Z,
Z,
A2. Commutativity: If  Z,
Z,
A3. Identity: If  Z,
Z,
If  Z,
Z,
A4. Inverses: If  Z,
Z,
II. Properties of Multiplication
M1. Associativity: If  Z,
Z,
M2. Commutativity: If  Z,
Z,
M3. Identity: If  Z,
Z,
III. Distributive Law
Addition and multiplication in Z are related by the distributive
law which asserts that if  Z,
Z,
At this point, let us cite some rules for calculating with integers. These rules are familiar from high school algebra and can easily be deduced from I, II, and III. Let  Z.
Z.
By way of illustration, let us prove (3). By A4, -y is the unique integer which has the property
The elements of the set
are called positive integers. The set P of positive integers is a subset of Z. Our next set of properties concerns the positive integers.
IV. Properties of Positive Integers
Exactly one of the following is true:
 P,
P, P.
P. P,
P, P.
P.
P0. Let  Z.
Z. P,
P, P.
P.
The set
is called the set of natural numbers.
Our last basic property of Z is the principle of mathematical induction.
V. Principle of Mathematical Induction
Let S be a nonempty subset of the set of positive integers P. Assume that
(a)  S
S
(b) whenever  S
S S.
S.
In more formal developments of the integers, the principle of mathematical induction is the basic tool available to prove theorems and, in fact, all the preceding basic properties may be deduced by using the principle of mathematical induction and a set of axioms for N called Peano's axioms.
The principle of mathematical induction can be used to prove theorems
as follows:Suppose that for each positive integer n, we have a given
proposition Pn. Suppose further that we are able to show that P1 is true and that whenever Pn is true, Pn+1 is true. Then Pn is true for every positive integer n. Indeed if  P | Pn is true},
P | Pn is true}, S,
S, S
S S,
S,
For each positive integer n there is a proposition Pn. Suppose also that
(a) P1 is true and that
(b) whenever Pm is true for all
V'. Variant of Mathematical Induction Principle
Suppose that for each positive integer n there is a proposition Pn. Suppose also that
(a) P1 is true and that
(b) whenever Pm is true for all
Then Pn is true for every positive integer n.
Let us illustrate the use of the principle of mathematical induction by means of a number of examples.
Example 1: Let us prove that in n is a positive integer, then
Let Pn denote this proposition. It is clear that P1 is true since
But then by adding n + 1 to both sides of the equation, we derive that
and thus Pn+1 is true. Thus, by the principle of mathematical induction, Pn is true for all  P
P
Example 2: Let S be a set containing n elements. Then S contains 2n subsets.
Denote this proposition by Pn. It is clear that P1 since if 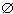 . Assume that Pn is true, and let
. Assume that Pn is true, and let  T
T
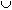 {an+1},...,T2n
{an+1},...,T2n
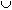 {an+1}.
{an+1}.
We have exhibited
Example 3: Definition by induction. It is possible to use
mathematical induction to define various mathematical concepts. The basic idea of this process of "definition by induction" is as follows: Suppose that it is required to define a function 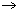 A,
A,
(a) specifying f(1) and
(b) specifying f(n + 1) in terms of f(1),f(2),...f(n).
If  P | f(n) is defined},
P | f(n) is defined},
By principle of mathematical induction, an is defined for n a positive integer or 0.
Example 4: Let  Z
Z
Feel free to complete the proof of these yourself.
Order
Let a and b be integers. We say that a is greater than b, denoted a>b, if a-b is a positive number. Thus, in particular, if  P,
P, P.
P.
Exactly on of the following holds:
O1. Exactly on of the following holds:
For, by P0, exactly one of the following holds:
In the first case
O2. If
O3. If
A simple application of O2 and O3 shows that there are no integers between 0 and 1. More precisely, we have
If b is a positive integer. Then b is greater than or equal to 1 Proposition 1: Suppose that b is a positive integer. Then b is greater than or equal to 1.
Proof: Let us proceed by induction. The assertion is clearly true for
Therefore by O2
which implies our assertion for b + 1. Therefore, the proposition is proved.
Let x and y be integers. If
Corollary 2: Let x and y be integers. If
Proof: If
We will require one additional basic property of inequalities:
If x < y and z > 0 then xz < yz.
If x < y and z < 0 then xz > yz.
O4a. If x < y and z > 0 then xz < yz.
O4b. If x < y and z < 0 then xz > yz.
For if  P,
P,
Another easy consequence of Proposition 1 is given by
Let a and b positive integers. Then there exists a positive integer n such that
Corollary 3: Let a and b positive integers. Then there exists a positive integer n such that
Proof: Set
A very important property of Z is the fact that if a and b are nonzero integers, then a · b is nonzero. The simplest way to see this is to divide the reasoning up into four cases: 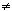 0.
0.
Theorem 4: Let a and b be nonzero integers. Then 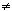 0.
0.
If S is a subset of Z, then an integer s is said to be the least(or smallest )element of S if  S
S S
S
Proposition 5: Let S be a finite, nonempty subset of Z. Then S has a largest and smallest element.
A somewhat more difficult result to prove is the well-ordering principle:
Theorem 6: Let S be a nonempty (finite or infinite) subset of N. Then S contains a smallest element.
Proof: The following argument makes a rather interesting use of the principle of mathematical induction. Let  N | y < x for all x
N | y < x for all x  S}.
S}.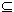 N,
N, S
S A
A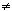
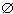 .
.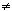 N.
N. S, then
S, then 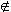 A.
A. A
A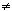 N,
N, A
A A.
A. A,
A, A,
A, A,
A, A,
A, S.
S. S.
S. A,
A, S
S S,
S, S.
S.
The Division Algorithm
Let a be a nonnegative integer and let b be a positive integer. In elementary arithmetic, we learned how to "divide" a by b, thereby deriving a quotient q plus a remainder of the form r/b, where
(10)This process of division can be expressed by the equation
(11)It is possible to formulate the process of division, as described by (10) and (11), solely in terms of integers.
Theorem 7(Division Algorithm): Let a be a nonnegative integer and let b be a positive integer. Then there exist natural numbers q and t such that
Proof: Of all the multiples
of b, there are only finitely many less than or equal to a. Indeed, Corollary 3 asserts that there exists a positive number n such that
since
The division algorithm, although it appears to be a rather superficial feature of the integers, is actually one of the most important results about Z. In other sections, we will see that the division algorithm can be applied in rather ingenious ways to yield arithmetic facts about the integers.