 b(mod n)
b(mod n) d(mod n),
d(mod n), (b+d)(mod n)
(b+d)(mod n) bd(mod n).
bd(mod n). b(mod n)
b(mod n) d(mod n),
d(mod n), (b+d)(mod n)
(b+d)(mod n) bd(mod n).
bd(mod n).| Back | Table of Contents |
|
|
Equivalence RelationsIn the section on congruences we introduced the notion of congruence of integers modulo n, and we proved the following basic properties of congruence:
1.
2. If
Moreover, we showed that the integers are distributed among the residue classes
1'. Every integer x belongs to one of the residue classes
2'. No integer belongs to two of the residue classes
i
 j = j =  (0 < i < j < n-1, i (0 < i < j < n-1, i  l). l).
Let us abstract from this data two very important notions - that of partition and equivalence relation.
Let S be a set. A partition of S is a collection
a.
b. If A and B are distinct elements of
For example, 1' and 2 ' assert that
1
2
3
The above example suggests the following definition: Let S be a set. Then a relation R on S is a subset of S
R = {(1,1), (1,2), (2,1),( 3,1)}
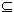 S S  S. S.
If R is a relation on S and if
R
 = {(x,y) = {(x,y) 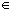 S S 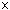 S | x ~C y}. S | x ~C y}.
In this case
ER1. For every 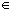 S S
ER2. If 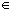 S S
ER3. If
The properties ER1-ER3 are called the reflexive, symmetric, and transitive laws, respectively. They completely characterize an equivalence relation, in the following
sense: Suppose there is given a relation R on S which satisfies rules ER1-ER3. Then it is possible to associate R on a partition 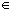 S | x ~R y}, S | x ~R y},
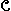 = {Ax | x = {Ax | x 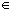 S}, S},
1.
2. R is the equivalence relation associated with
It is clear that 2 holds provided 1 does. Thus it suffices to prove 1. Since 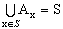
Assume that
Ax
 Ay Ay  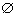
We must show that
x ~R z, y ~R z, x ~R w.
Therefore, by ER2,
x ~R z, z ~R y, w ~R x.
w ~R x, x ~R y.
which implies that Note: The reader should carefully master the relationship between a partition and an associated equivalence relation, since this idea will be used over and over later.
If ~ is an equivalence relation and
Equivalence relations occur with surprising frequency in even the most innocent of contexts. For example, consider the rational numbers (or fractions). From our days in grade school, we
are accustomed to thinking of a rational number as the quotient a/b of integers a and b
a/b ~ c/d
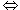 ad - bc = 0. ad - bc = 0.
It is easy to verify that ~ is an equivalence relation and that all the ratios a/b, 2a/2b, 3a/3b, etc., are equivalent to one another. Then a rational number can be defined to be an equivalence class belonging to ~. Roughly speaking a rational number is the "common value" of the ratios
{a/b, 2a/2b, (-1)a/(-1)b, 6a/6b, ...},
Suppose that A is a set and ~ is an equivalence relation over A. Moreover, suppose that * is a binary operation on A. We will say that * is compatible with ~ if, whenever
If A is a set and ~ is an equivalence relation on A, let
Ax *' Ay = Ax*y.
Please note that in order for (2) to define a binary operation on In what follows, we will give many examples of equivalence relations on various algebraic structures (for example, groups, rings) and of binary operations compatible with these relations, so we will refrain from giving further examples at this point. |
| Back | Table of Contents |