A commutative ring R is an integral domain if R contains no zero divisors. In other words, R is an integral domain if the product of any two nonzero elements of R is nonzero. A function f : AmapsB is said to be surjective (or onto) if for every y element of B there exists x element of A such that f(x) = y. a commutative group> The set of integers. The set of rational numbers. Let R and S be rings, f :mapsS a ring homomorphism, then (1) ker(f ) is an ideal of R. and (2) f is an isomorphism if and only if ker(f ) = {0}. Let R and S be rings. A ring homomorphism from R to S is a function f :RmapsS such that for a,b element of R, we have (a). f(a + b) = f(a) + f(b), (b). f(a · b) = f(a) · f(b). If <f is also injective, f is a ring isomorphism
Back | Table of Contents

Two Useful Theorems

In this section we prove two extremely useful results concerning rings, both of which make use of the notion of embedding.

Definition 1: Let R and S be rings. We say that R is embedded in S if there exists an isomorphism f :RmapsS. The isomorphism f is said to be an embedding of R in S.

If R is embedded in S via the embedding f, then f(R) is a subring of S and f is a surjective isomorphism of R onto f(R). Therefore, Risomorphic tof(R). We may identify R with f(R) and therefore view R as a subring of S.

In the concept of rings section, we saw that 2Z is a ring without an identity element. Note, however, that 2Z can be embedded in Z, which is a ring with identity. Our first result shows that this is quite a general phenomenon.

Theorem 2: Let R be a ring. Then R can be embedded in a ring with identity.

Before proceeding with the proof of Theorem 2, let us define a general notion which will come up rather frequently in our studies. Let R be a ring and let r element of R, n element of Z. We seek to define the product n · r. Set

r n times if n > 0
= 0                if n = 0
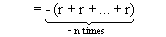negative r n times if n < 0

Note that n · r is just the "nth power of r" in the additive group of R. This is also referred to as the scalar product. Therefore, the following properties of n · r are just restatements of the laws of exponents in an abelian group.

(1)
n · (r1 + r2) = n · r1 + r2,
(2)
n(-r) = -(n · r),
(3)
(n1 + n2) · r = n1 · r + n2 · r,
(4)
(n1 · n2)· r = n1 · (n2 · r),
(5)
1 · r = r.

It should be noted however that in general the product ab for a and b in R and the scalar product nr are two different concepts entirely. The concept of scalar multiplication is derived from a shorthand notation fro certain statements about addition.

Proof of Theorem 2: Let us consider the Cartesian product

R cross Z = {(r,n) | r element of R, n element of Z}.

Let us define addition and multiplication on R cross Z by

(r1,n1) + (r2,n2) = (r1 + r2, n1 + n2),
(r1,n1)·(r2,n2) = (r1·r2 + n1·r2 + n2·r1, n1·n2).

Then, with respect to these operations, R cross Z is a ring. Moreover, R cross Z has an identity (0,1), since

(r1,n)·(0,1) = (r1· 0 + n · 0 + 1 · r1, 1 · n) = (r1,n),
(0,1)·(r1,n) = (0 · r1 + 1 · r1 + n · 0, 1 · n) = (r1,n).

Define the mapping

f :RmapsR cross Z,
f(r) = (r,0).

Then

f(r1 + r2) = (r1 + r2, 0) = f(r1) + f(r2),
f(r1·r2) = (r1·r2,0) = f(r1)·f(r2).

Therefore, f is a ring homomorphism. Moreover, ker(f = {0}, so that f is an isomorphism by Proposition 7 of the previous section. Therefore, R is embedded in the ring with identity R cross Z via the embedding f.

Let us now pose the following problem: Can an integral domain D always be embedded in a field? In order to get a good feel for the problem as well as its solution, let us consider the special case D = Z. In this special case, we know that the answer is yes since Zsubset ofQ, the field of rational numbers, and the mapping i:ZmapsQ defined by i(x) = x is an embedding of Z into Q. In order to understand the relationship between Z and Q, let us examine how Q can be gotten from Z. Roughly speaking, Q is gotten by forming "quotients" a/b of elements a,b element of Z, bnot equal0. However, different quotients can represent the same element of Q. For example, 2/3 = 4/6 = 6/9, etc. The element a element of Z is viewed as the quotient a/1, and the embedding i is actually the mapping i(a) = a/1. Note that every element of Q is of the form i(a)i(b)-1 (a,b element of Z, bnot equal0), since

a/b = (a/1)(b/1)-1.

Our goal in the second theorem is to generalize these facts to the case of an arbitrary integral domain in place of Z. Our main result is the following theorem.

Theorem 3: Let R be an integral domain. There exists a field FR and an embedding f :RmapsFR such that every element of FR is of the form f(a)·f(b)-1 (a,b element of R, bnot equal0). (FR is called the quotient field of the integral domain R.)

Proof: Let us mimic the situation in the case of the rational numbers. Let

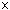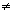S = {(a,b) element of R cross R | bnot equal0},

and let ~ denote the relation defined on S defined by

(a,b) ~ (c,d) equivalent to ad - bc = 0.

Then ~ is an equivalence relation on S. Let FR denote the set of equivalence classes of S with respect to ~, and let us denote the equivalence class containing (a,b) by a/b. (The above construction is necessary to guarantee that the fractions a/b and ac/bc are equal.) We define addition and multiplication of FR by

a/b + c/d = (ad + bc)/bd,
(a/b) · (c/d) = (a · c)/(b · d).

Note that bdnot equal0 since bnot equal0, dnot equal0, and R is an integral domain.

Let us prove that these operations are consistent. By way of example, let us supply the details only in the case of addition. Suppose that a/b = a'/b', c/d = c'/d'. Let us show that

(6)
a/b + c/d = a'/b' + c'/d'.

Indeed, a/b + c/d = (ad + bc)/bd, a'/b' + c'/d' = (a'd' + b'c')/b'd'. Moreover, since a/b = a'/b', we see that ab' = a'b. Similarly, cd' = c'd. The statement (6) is equivalent to

(7)
(ad + bc)b'd' = (a'd' + b'c')bd.

But, (ad + bc)b'd' = ab'dd' + b'bcd = a'bdd' + b'bc'd = (a'd' + b'c')bd, which proves (7). Thus addition is consistent. The proof for multiplication is similar.

The mapping

f :RmapsFR,
f(r) = r/1

is an embedding. Moreover, if a/b element of FR, then

a/b = (a/1)·(1/b) = (a/1)·(b/1)-1
= f(a) · f(b)-1.

Thus, FR satisfies the conditions of the theorem.

Usually, we will dispense with the embedding f and will merely identify r element of R with the element r/1 element of FR. Then R becomes a subring of FR.

Example 1: If R = Z, then FR = Q.

Example 2: Let R = F[X]. Then

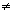FR = {f/g | f, g element of F[X], gnot equal0}.

Two elements, f/g and f'/g', of FR are equal if and only if

fg' = f'g.

The two elements of FR are called rational functions in X.
Back | Table of Contents