The Concept of a Ring
Definition 1: A ring is a nonempty set R on which there are defined two binary operations + and ·, which satisfy the following axioms:
R1. With respect to +, R is an abelian group.
R2. · is associative:a · (b · c) = (a · b) · c for all  R.
R.
R3. The following distributive laws are satisfied:
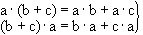 for all a, b, c
for all a, b, c  R.
R.
The operation + is called addition and the operation · is called multiplication.
In a ring R, we will denote the identity with respect to addition by 0, and we will denote the inverse of a with respect to + by -a. We will call the identity with respect to addition the zero element of R or just zero
Note that although we have assumed that R contains a an identity with respect to addition, we have made no such assumption with regards to multiplication. An identity element i with respect to multiplication is an element of R such that
for all a  R. A given ring may or may not contain such an element. We will give examples of both phenomena below. However, if i and i' are two identity elements with respect to multiplication, then we must have
R. A given ring may or may not contain such an element. We will give examples of both phenomena below. However, if i and i' are two identity elements with respect to multiplication, then we must have
Therefore, any two identities of R are equal and R contains at most one identity with respect to multiplication.
Definition 2: Let R be a ring. If R contains an identity with respect to multiplication, then we say that R is a ring with identity. The unique identity with respect to multiplication will be denoted 1R (or just 1 if R is clear from context) and will be call the identity of R. (Note that some texts require that all rings have an identity. We will adopt that convention later.)
We will see below that the operation of multiplication need not satisfy the commutative law. Therefore, let us make the following definition.
Definition 3: Let R be a ring. We say that R is a commutative ring if
for all a, b  R.
R.
Let us now get some feel for the variety of possible rings by studying a number of examples.
Example 1: Let R = Z, with respect to the usual operations of addition and multiplication. Then as mentioned at the outset, all the ring axioms are verified. The ring Z is commutative and has identity 1.
Example 2: Let R = Q, the set of all rational numbers, and let addition and multiplication, respectively, be addition and multiplication of fractions. With respect to these operations, Q becomes a ring. Then ring Q is commutative and has identity 1.
Example 3: Let R = R, the set of all real numbers. Let addition and multiplication be addition and multiplication of real numbers. Then R becomes a commutative ring with identity 1.
Example 4: Let  Z}
Z} R
R
Then, with respect to the usual operations of addition and multiplication of integers, rZ is a commutative ring having no identity unless
Example 5: Let
Then the axioms R1-R3 are satisfied in a trivial way. Thus, R is a ring called the trivial ring. Note that R is a commutative ring with identity 0. Thus, in this example,
Example 6: Let R = Zn for some positive integer n, and let addition and multiplication be defined as addition and multiplication of residue classes. It was established earlier that R1-R3 are satisfied, so that R becomes a ring. Note that R is a finite ring with n elements. Moreover, R is commutative with 1. The most peculiar property exhibited by some of the rings Zn is that it often happens that the product of two nonzero elements of Zn equals 0, which is the zero element of Zn. For example, consider  Z6.
Z6. 0,
0, 0,
0,
Example 7: Let R denote the set of functions 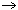 R.
R. R,
R,
 R),
R),
For example, if  R.
R. R,
R, R.
R. R
R
 0), f(0) = 1,
0), f(0) = 1, 0), g(0) = 0.
0), g(0) = 0.
Then  0,
0, 0,
0,
Example 8: Let R be the set of all functions f :R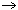 R of the form
R of the form
 R).
R).Such a function is called a polynomial function. Let addition and multiplication of functions be defined as in Example 7. Then the sum (and product) of two polynomial functions is again a polynomial function, so we have two binary operations defined on R. With respect to these operations, R is a commutative ring with identity.
Example 9: Let R denote the set of all 2 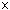 2 matrices with real entries. A typical element of R looks like
2 matrices with real entries. A typical element of R looks like
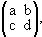
where  R.
R.
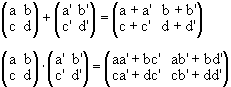
With respect to these operations, R becomes a ring with identity. The zero element and the identity of R are given by
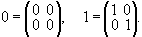
Note that
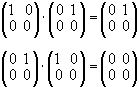
Therefore, R is not a commutative ring. We will henceforth denote the ring of 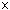 2
2
Example 10: Let d be an integer, and let R consist of the set of all complex numbers of the form 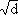 ,
, Z.
Z.
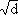 ) + (a' + b'
) + (a' + b'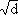 ) = (a + a') + (b + b')
) = (a + a') + (b + b')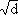 ,
,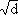 )(a' + b'
)(a' + b'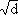 ) = (aa' + bb'd) + (ab' +ba')
) = (aa' + bb'd) + (ab' +ba')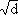 ,
,
we see that addition and multiplication define binary operations on R. The fact that R forms a ring is now trivial to verify from the properties of the complex numbers. The ring R will be denoted Z[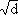 ].
].
Example 11: Let R be the set of all complex numbers of the form 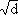 ,
, Q.
Q.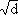 ].
].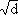 ).
).
Example 12: Let R and S be any two rings, and let 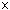 S
S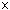 S
S
Then it is easy to verify that 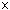 S
S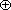 S.
S.
Now that we have surveyed the wide possibilities, which the ring axioms create, let us establish some elementary properties of rings. The following proposition will start us along that line.
Proposition 4: Let R be a ring.  R.
R.
(1) a · 0 = 0 · a = 0.
(2) a · (-b) = (-a) · b = -(a · b).
(3) (-a) · (-b) = a · b.
Note that these rules of arithmetic in an arbitrary ring are just generalizations of well-known facts from the algebra of the integers, Z.
Proof:
(1) Since 0 is the identity with respect to addition,
Therefore, by adding -(a · 0) to both sides of this last equation, we get
(2) Let
(-a) · b = (-a) · b + 0
= (-a) · b + [a · b + y]
= (-a + a) · b + y (by associative and distributive laws)
= 0 · b + y (since -a + a = 0)
= 0 + y (by (1))
= y.
Therefore, (-a) · b = -(a · b).
(3) By part (2),
(-a) · (-b) = -a · (-b)
= -(-a · b)
= a · b (since R is a group with respect to addition)
Let us now examine some of the phenomena which were exhibited by our examples. In Examples 6 and 7 we found that there exist nonzero ring elements a and b such that
Definition 5: Let R be a ring,  R,
R, 0.
0. R,
R, 0, such that
0, such that
If R is a commutative ring, then the distinction between right and left zero divisors disappears. An element of a commutative ring R is a right zero divisor if and only if it is a left zero divisor.
Definition 6: A commutative ring R is said to be an integral domain if R contains no zero divisors. In other words, R is an integral domain if the product of any two nonzero elements of R is nonzero. (For convenience in stating various results, we will always assume that an integral domain always contains an identity.)
For example Z6 is not an integral domain because 2 is a zero divisor. Similarly, Example 7 shows the ring of functions 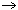 R
R 0.
0.
Proposition 7: Suppose that R is an integral domain,  R,
R, 0.
0.
Proof: By Proposition 4 and the distributive law, we have
However, since  0
0
If R is a ring with identity 1, it makes sense to ask whether an element a of R has an inverse with respect to multiplication. That is, does there exist  R
R
If such an element b exists, it is unique. We have already worked through this sort of argument several times, and therefore we will leave the verification that b is unique as an exercise for the reader. If a has an inverse with respect to multiplication, then the unique inverse will be denoted a-1.
Definition 8: Let R be a ring with identity 1, and let  R.
R.
Example 13: Let R be any ring with identity. Then 1 and -1 are units. In fact, since
Example 14: Let  R
R R
R
Example 15: Let  1
1 R.
R. Q - {0},
Q - {0},
we see that (a/b)-1 = b/a.
Example 16: Let R = the trivial ring. Then, since
Example 17: Let R be any ring with identity which is not the trivial ring. In this ring  0.
0.
However,  0
0 0.
0. R,
R, 1.
1.
Example 18: Let 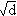 | a,b
| a,b  Z}
Z}
d = -1: 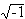 ,
,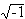 ,
,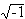 ,
,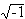
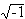 ,
,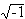 ,
,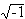 ,
,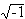 .
.
d = 2: 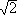 ,
,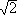 ,
,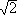 ,
,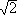 ,
,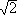 ,
,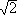 ,
,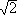 ,
,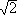
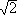 ,
,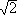 ,
,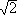 ,
,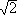 ,
,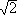 ,
,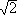 ,
,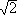 ,
,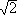
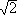 )n
)n
It is worthwhile to record the observation made in example 17 as a proposition.
Proposition 19: Let R be a ring with identity which is not the trivial ring. Then  0R.
0R.
For any ring with identity, let us denote by UR the set of all units of R. From our above examples, we know that  UR
UR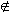 UR.
UR.
Proposition 20: Let R be a ring with identity, and let  UR.
UR.
(1) a-1  UR.
UR.
(2)  UR
UR
(3) UR is a group with respect to multiplication.
Proof:
(1) Since a  UR, a has an inverse a-1 and
UR, a has an inverse a-1 and
(2) Since
These last two equations show how
(3) By part (2), UR is closed with respect to multiplication. Moreover, we observed above that  UR,
UR, UR,
UR,
The group UR is called the group of units of R.
In order to introduce the last of special classes of rings which we will examine in this section, let us confine our discussion to a ring R with identity which is not the trivial ring. Let us denote the subset 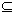 Rx.
Rx.
Definition 21: A field is a nontrivial commutative ring with identity in which every nonzero element has an inverse with respect to multiplication.
Note that a field must contain at least two elements, since it is a nontrivial ring. Therefore, in particular, in a field, we have  0.
0.
Example 22: A a result of our previous discussion, we see that Q is a field.
Example 23: R, the set of real numbers, is a field.
Example 24: Let p be a prime and let Zp denote the ring of residue classes modulo p. Recall that
Proposition 25: Let F be a nontrivial commutative ring with identity. Then F is a field if and only if Fx is a group with respect to multiplication.
Proof:  . Assume that F is a field. Then by definition of a field
. Assume that F is a field. Then by definition of a field
 . Assume that Fx is a group. Then every element of Fx has an inverse with respect to multiplication. Therefore, F is a field.
. Assume that Fx is a group. Then every element of Fx has an inverse with respect to multiplication. Therefore, F is a field.
Corollary 26: Let F be a field. Then F is an integral domain.
Proof: If F is a field, then FX is a group. Fx is closed with respect to multiplication. Therefore, F is an integral domain.
The extreme importance of fields in mathematics is due to the fact that in a field it is possible to combine elements using all the operations which one meets in elementary arithmetic. That is, given any two elements a and b of a field, it is possible to form their sum  0,
0,
If R is a ring with identity, then it is convenient to introduce the language of exponents in R. Let  R,
R,
Then the following laws of exponents hold:
(1)Moreover, if R is commutative, then
(3)Another useful definition is:
Definition 27:The characteristic of a ring R (written Char R) is the smallest positive integer such that n1 = 0,where n1 is an abbreviation for  0.
0. 0,
0,