 W
W W
W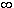 Let W
Let W 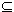 V. Then W is of subspace of V
V. Then W is of subspace of V  For all
For all  W,
W,
 F,
F, W,
W, w
w  W.
W. H is a homomorphism. The kernel of f is ker(f) = {x
H is a homomorphism. The kernel of f is ker(f) = {x  G | f(x) = 1H}.
Let G1 and G2 be groups. An isomorphism from G1 to G2 is an injection
G | f(x) = 1H}.
Let G1 and G2 be groups. An isomorphism from G1 to G2 is an injection  :G1
:G1 G2
G2 (a · b) =
(a · b) =  (a) ·
(a) ·  (b) (a,b
(b) (a,b  G1).
Let
G1).
Let  H
H ker(f) = {1G}.
ker(f) = {1G}.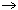 H
H G
G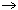 B
B B
B A
A| Back | Table of Contents |
|
|
Linear TransformationsIn this section we will again pursue the analogy between vector spaces, on the one hand, and groups and rings on the other, by defining an analogue of the homomorphisms of group theory and ring theory. In the case of vector spaces, the homomorphisms are called linear transformations (or linear operators).
Definition 1: Let V and W be vector spaces over the same field F. A linear transformation from V to W is a function
T(v + v') = T(v) + T(v'),
(2)
T(
 v) = v) =  T(v). T(v).Note that a linear transformation
T(v - v') = T(v) - T(v').
Let v1,...,vn
T(
 1v1 + ... + 1v1 + ... +  vn) = vn) =  1T(v1) + ... + 1T(v1) + ... +  nT(vn). nT(vn).Example 1: Let Example 2: Let V and W be finite-dimensional vector spaces over the field F and let {e1,...,en}, {f1,...,fm} be bases for V and W, respectively. Let
T(ei) = a1if1 + ... + amifm (1 < i < n),
where
v =  1e1 + ... + 1e1 + ... +  nen, nen,  i i  F. F.
Therefore, by (4),
T(v) =
(5)
 1T(e1) + ... + 1T(e1) + ... +  nT(en) nT(en)
=
 1(a11f1 + ... + am1fm)+ ... + 1(a11f1 + ... + am1fm)+ ... + n(a1nf1 + ... + amnfm) n(a1nf1 + ... + amnfm)
= (a11
 1 + a1n 1 + a1n n)f1 + ... + (am1 n)f1 + ... + (am1 1 + ... + amn 1 + ... + amn n)fn. n)fn.Thus, the image of any vector v with respect to T is completely determined by the set {aij}. Conversely, given any set with {aij} of mn elements of F, formula (5) defines a linear transformation of V into W. Example 3:
f = a0 + a1X + ... + anXn
 F[X], F[X],let us define the formal derivative of f, denoted Df, by
Df = 1 · a1 + ... + n · anXn-1.
Then Example 4: Let C[0,1] = the vector space over R of all continuous functions
T(f ) =
 f(x)dx. f(x)dx.Then, by the properties if the integral proved in calculus, we have
T(f + g) =
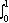 ( f(x) + g(x))dx ( f(x) + g(x))dx
=
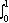 f(x)dx + f(x)dx + 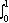 g(x)dx g(x)dx
= T(f ) + T(g),
T(
 f ) = f ) = 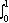  f(x)dx f(x)dx
=
 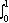 f(x)dx f(x)dx
=
 T(f ) T(f )
for all As in group theory, and ring theory let us define the kernel of the linear transformation
ker(T) = {v
 V | T(v) = 0}. V | T(v) = 0}.
Proposition 2: Let (1) T(V) is a subspace of W. (2) ker(T) is a subspace of V. Proof: (1) Let
w - w' = T(v) - T(v') = T(v - v')
 T(V). T(V).
since  w = w =  T(v) = T( T(v) = T( v) v)  T(V), T(V),
since
T(v - v') = T(v) - T(v')
= 0 - 0
= 0
And, by (2),
T(
 v) = v) =  T(v) = T(v) =  0 = 0 0 = 0
Thus, Let
Proposition 3: T is an isomorphism In our discussion of groups we remarked that one of the fundamental goals of the theory of finite groups is to make a list of all nonisomorphic finite groups, this goal being beyond the present state of knowledge. In the case of vector spaces, however, the situation is far different. The following theorem gives a complete classification of all finite-dimensional vector spaces over a field F
Theorem 4: Let V be a finite-dimensional vector space over a field F and let Proof: Let {e1,...,en} be a basis of V. Then every vector
v =
 1e1 + ... + 1e1 + ... +  nen. nen.
Define the function
T(
 1e1 + ... + 1e1 + ... +  nen) = ( nen) = ( 1,..., 1,..., n). n).
It is easy to check that T is a linear transformation and T is clearly surjective. If
T(v) = 0
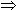 ( ( 1,..., 1,..., n) = (0,...,0) n) = (0,...,0)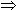  1 = 1 =  2 = ... = 2 = ... =  n = 0 n = 0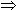 v = 0. v = 0.
Thus, by Proposition 3, T is an isomorphism. Therefore,
Theorem 5: Let V and W be vector spaces over F, and let (1) dimF(T(V)) < dimF(V) (2) If T is an isomorphism, dimF(T(V)) = dimF(V). Proof: (1) Without loss of generality, let us assume that V is finite-dimensional, and let {e1,...,en} be a basis of V. Then
V = {
 1e1,..., 1e1,..., nen | ai nen | ai  F}, F},so that
T(V) = {
 1T(e1) + ... + 1T(e1) + ... +  nT(en) | nT(en) |  i i  F}, F},
and thus {T(e1),...,T(en)} is a set of generators for (2) Let the notation be as in the proof of (1). It suffices to show that {T(e1),...,T(en)} is a basis for
0 =
 1T(e1) + ... + 1T(e1) + ... +  nT(en). nT(en).
0 = T(
Theorem 5 has an interesting application to the theory of simultaneous linear equations. Let us consider the following system of equations:
a11x1 + a12x2 + ... + a1mxm = b1
a21x1 + a22x2 + ... + a2mxm = b2
.
(7)
.
.
an1x1 + an2x2 + ... + anmxm = bn,
where aij, bi all belong to a given field F. A solution of the system (7) is an m-tuple (x1,...,xm) Theorem 6: Let
a11x1 + a12x2 + ... + a1mxm = 0
a21x1 + a22x2 + ... + a2mxm = 0
.
(8)
.
.
an1x1 + an2x2 + ... + anmxm = 0,
be a homogeneous system with coefficients aij belonging to the field F. If Proof: Consider the linear transformation
T((x1,...,xm)) = (0,...,0)
Assume that (8) has only the zero solution. Then
However, since |
| Back | Table of Contents |