The Concept of a Vector Space
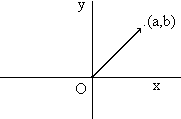
In physics one often meets physical quantities which have both a magnitude and a direction. For example, a force is described by its magnitude and the direction in which it is applied. Such quantities are often called vectors by the physicist. For simplicity, we will confine our discussion to vectors in two dimensions. A convenient representation of a vector quantity can be obtained by drawing an arrow from the origin of a rectangular coordinate system in the direction of the vector, where the length of the arrow equals the magnitude of the vector (see Figure 1). It is a short abstract jump to replace the arrow by the ordered pair
Suppose that forces F1 and F2 are applied to a body. Experiment has shown the physicist that the resulting force, which is called the sum of F1 and F2, is the same as the force described by constructing a parallelogram with F1 and F2 as the sides and taking the diagonal of this parallelogram (see Figure 2). Thus if F1 and F2 correspond to the ordered pairs
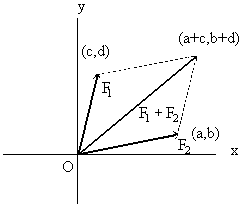
The mathematician interprets addition of vectors as follows: Let V2 denote the set of all ordered pairs  R).
R).
It is trivial to verify that with respect to this operation, V2 is an abelian group. The identity element is
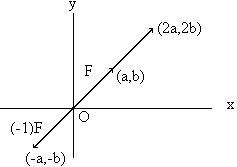
In addition to the operation + among vectors, there is another natural operation present. If F is a vector and  is a real number, then it is possible to "multiply"
is a real number, then it is possible to "multiply"  and F as follows:
and F as follows:  F is the vector whose magnitude is
F is the vector whose magnitude is  | · |F|,
| · |F|, F is the same as the direction of F if
F is the same as the direction of F if  > 0,
> 0, < 0
< 0 F corresponds to
F corresponds to  a,
a, b).
b). ,
,
 R,
R, V2,
V2,
 +
+  ) · v =
) · v =  · v +
· v +  · v,
· v, · (v + w) =
· (v + w) =  · v +
· v +  · w,
· w,
 ) · v =
) · v =  · (
· ( v),
v),
For example, let us prove (1): Let
 +
+  ) · v = (
) · v = ( +
+  ) · (a · b)
) · (a · b) +
+  )a, (
)a, ( +
+  )b)
)b) a +
a +  a,
a,  b +
b +  b)
b) a,
a,  b) + (
b) + ( a,
a,  b)
b) · (a,b) +
· (a,b) +  · (a,b)
· (a,b) · v +
· v +  · v.
· v.The proofs of (2) - (4) are similar.
We have just created a new algebraic system. The vectors in two dimensions form an abelian group with respect to addition, but they also admit multiplication by a set of elements known as scalars, such that the properties (1)-(14) are satisfied. Such an algebraic system is called a vector space. Let us now formally define this concept.
Definition 1: Let F be a field. A vector space over F is a nonempty set V plus two functions  V
V  V,
V, V
V  V,
V,
V1. With respect to vector addition, V is an abelian group.
V2. For all 
 F,
F, V,
V, · (v + w) =
· (v + w) =  · v +
· v +  · w.
· w.
V3. For all  ,
,
 F,
F, V,
V, +
+  ) · v =
) · v =  · v +
· v +  · v.
· v.
V4. For all  ,
,
 F,
F, V,
V, · (
· ( · v) = (
· v) = ( ·
·  ) · v.
) · v.
V5. For all  V,
V,
The elements of V are called vectors and the elements of F are called scalars.
Example 1: F = R, V = V2. Then V2 is a vector space over R.
Example 2: Let F be any field.  F, 1 < i < n}.
F, 1 < i < n}.
Define scalar multiplication by
 · (a1,...,an) = (
· (a1,...,an) = ( a1,...,
a1,..., an) (
an) (
 F).
F).Then with respect to these operations, V becomes a vector space over F, denoted Fn.
Example 3: Let F be any field, 
 F,
F, F[X].
F[X].
 · f =
· f =  a0 + (
a0 + ( a1)X +...+ (
a1)X +...+ ( an)Xn.
an)Xn.
Then with respect to these operations,
Example 4: Let F be any field,  F[X] | deg(f ) < n},
F[X] | deg(f ) < n},
Example 5: Let
 [0,1]),
[0,1]),and define scalar multiplication by
 f)(x) =
f)(x) =  f(x) (x
f(x) (x  [0,1]).
[0,1]).
Then
Example 6: Let E be a field, F a subfield of E. Let
Thus, we see from the above examples that a great variety of mathematical objects qualify as vector spaces. The notion of a vector space is one of the fundamental unifying notions in modern mathematics, both pure and applied, and finds applications in fields as diverse as psychology and quantum mechanics.
Some Remarks: 1. If V is a vector space with vector addition +, then V is an abelian group with respect to +. In order to minimize confusion, we will always use additive notation with respect to this group. The identity element will be denoted 0, whereas the inverse of v will be denoted -v. Note that 0 is not the same as  F.
F.
2. Vectors will always be denoted by lower case Roman boldface letters, for example v,w,x,y. Scalars will be denoted by lower case Greek letters, for example  ,
, ,
, ,
, .
.
3. We will usually omit the · signifying scalar multiplication and will write  v instead of
v instead of  · v.
· v.
4. The reason for the axiom  V)
V) v = 0
v = 0 V,
V,
Three elementary, but useful, facts concerning vector spaces are
(5) V),
V), V),
V), (-v) = (-
(-v) = (- )v = -(
)v = -( v) (
v) (
 F, v
F, v  V),
V),