|
Basis and Dimension
In the preceding section, we observed that S = {e1, e2, ..., en} where
e1 = (1,0,0,...,0)
e2 = (0,1,0,...,0)
·
·
·
en = (0,0,0,...,1)
is a set of generators for the vector space Fn. Thus, every element v of Fn can be written in the form
(1)
Actually, the set S of generators has a very special property: The elements  i in (1) are uniquely determined. Indeed, i in (1) are uniquely determined. Indeed,
so that if (1) holds, and v = (v1, ..., vn), then  i = vi (1 < i < n). i = vi (1 < i < n).
Definition 1: Let V be a vector space over F. A basis of V is a subset {ei} of V (finite or infinite) with the property that every element v of V can be uniquely written in the form
v = 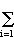  iei iei.
(Here we always assume that if {ei} is infinite, then  i = 0 for all but a finite number of i, also that the sum is a finite sum.) i = 0 for all but a finite number of i, also that the sum is a finite sum.)
Example 1: {ei, ..., en} is a basis for Fn.
Example 2: {e1 - e2,e1 + e2} is a basis for F2 since v = (v1,v2, then
v = (v1 - v2)/2(e1 - e2) + (v1 + v2)/2(e1 + e2),
and if v =  (e1 - e2) + (e1 - e2) +  (e1 + e2), then v = ( (e1 + e2), then v = ( + +  , ,  - -  ), so that ), so that  = (v1 - v2)/2, = (v1 - v2)/2,  = (v1 + v2)/2. Thus, every element of F2 can be represented in one and only one way in the form = (v1 + v2)/2. Thus, every element of F2 can be represented in one and only one way in the form  (e1 - e2) + (e1 - e2) +  (e1 + e2), so that {e1 - e2, e1 + e2} is a basis of F2. (e1 + e2), so that {e1 - e2, e1 + e2} is a basis of F2.
The main goal of this section is to show that any two bases of a vector space V have the same number of elements, in the following sense: If one basis of V has a finite number of elements, then every basis has a finite number of elements, and every basis has the same number. If one basis of V is infinite, then every basis is infinite. Assuming this result for the moment, let us make the following definition.
Definition 2: Let V be a vector space. If V has a finite set of generators, then we say that V is finite-dimensional and we define its dimension, denoted dimFV, to be the minimum possible number of elements in such a set. If V does not have a finite set of generators, then we say the V is infinite-dimensional, and we define dimFV to be 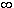 . .
For example, let V = {0}. Since S = 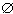 is a set of generators for V, and since S is clearly as small as possible a set of generators, we see that dimFV = 0. is a set of generators for V, and since S is clearly as small as possible a set of generators, we see that dimFV = 0.
Assume no that V 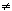 {0} and that V is finite-dimensional. Let S = {v1, ..., vn} be a set of generators having as few elements as possible. (Since V {0} and that V is finite-dimensional. Let S = {v1, ..., vn} be a set of generators having as few elements as possible. (Since V 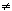 {0}, S is nonempty.) Then by definition of dimFV, we have dimFV = n. We will show that {v1,..., vn} is a basis of V. Indeed, Since S generates V, every element v of V can be written in the form {0}, S is nonempty.) Then by definition of dimFV, we have dimFV = n. We will show that {v1,..., vn} is a basis of V. Indeed, Since S generates V, every element v of V can be written in the form
v =  v1 v1 + ... +  nvn nvn (  i i  F).
We assert that this representation is unique. For if v =  1v1 + ... + 1v1 + ... +  nvn with nvn with  1 1 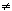  1, say, 1, say,  1 - 1 -  1 1 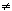 0 and 0 and
v1 =  2v2 2v2 + ... +  nvn nvn,
where  i = ( i = ( 1 - 1 -  1)-1( 1)-1( i + i +  i) (2 < i < n). But w i) (2 < i < n). But w  V, we may write V, we may write
w =  1v1 1v1 + ... +  nvn nvn, (  i i  F)
= (  2 2 +  1 1 2 2) v2 + ... + (  n n +  1 1 n n) vn,
so that w can be written as a linear combination of v2, ..., vn. Then, since w  V is arbitrary, {v2, ..., vn} is a set of generators for V, which contradicts the hypothesis that S is as small as possible. Thus the representation is unique, and S is a basis for V. We have shown that the dimension of V can be computed as the number of elements in a set of generators that is as small as possible and such a set of generators is a basis for V. We will show next that any two bases of V have the same number of elements. Thus, we will have prove that dimFV = the number of elements in a basis for V. By the way, we should remark that it is a consequence of our above reasoning that every nonzero finite-dimensional vector space has a basis. (Just take as a basis any set of generators that is as small as possible.) For example, dimFFn = n, since {e1, ..., en} is a basis for Fn. V is arbitrary, {v2, ..., vn} is a set of generators for V, which contradicts the hypothesis that S is as small as possible. Thus the representation is unique, and S is a basis for V. We have shown that the dimension of V can be computed as the number of elements in a set of generators that is as small as possible and such a set of generators is a basis for V. We will show next that any two bases of V have the same number of elements. Thus, we will have prove that dimFV = the number of elements in a basis for V. By the way, we should remark that it is a consequence of our above reasoning that every nonzero finite-dimensional vector space has a basis. (Just take as a basis any set of generators that is as small as possible.) For example, dimFFn = n, since {e1, ..., en} is a basis for Fn.
Definition 3: Let S 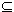 V be a nonempty subset of V. Then S is said to be linearly dependent if there exist distinct elements s1, ..., sn belonging to S and V be a nonempty subset of V. Then S is said to be linearly dependent if there exist distinct elements s1, ..., sn belonging to S and  1, ..., 1, ...,  n belonging to F, not all 0 such that n belonging to F, not all 0 such that
 1s1 1s1 +  2s2 2s2 + ...+  nsn nsn = 0.
If S is not linearly dependent, then we say that S is linearly independent.
Example 3: Let V = R2, S = {e1, 2e1}. Then S is linearly dependent since
(-2) · e1 + 1 · (2e1) = 0.
Example 4: Let V be arbitrary and let S = {0}. Then is linearly dependent since 1 · 0 = 0.
Example 5: Let V be arbitrary and let S be a basis of V. Then S is linearly independent, since if
 1s1 1s1 +  2s2 2s2 + ... +  nsn nsn = 0,  i i  F, si  S,
then since
0 = 0 · s1 + 0 · s2 + ... + 0 · sn,
the fact that 0 is uniquely representable in terms of the basis implies that  1 = 1 =  2 = ... = 2 = ... =  n = 0. n = 0.
Proposition 4: Let V be a vector space and let S 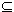 V be a nonempty subset. Then S is a basis for V if and only if S is a set of generators for V and S is linearly independent. V be a nonempty subset. Then S is a basis for V if and only if S is a set of generators for V and S is linearly independent.
Proof: If S is a basis, then S is clearly a set of generators for V. Moreover, S is linearly independent by Example 5 above. If S is a basis, then S is clearly a set of generators for V. Moreover, S is linearly independent by Example 5 above.
 Let v Let v  V/ Since S is a set of generators, there exist V/ Since S is a set of generators, there exist  s (s s (s  S) belonging to F such that S) belonging to F such that
(2)
v =   ss ss,
where all but a finite number of the  s are 0. Let us show that the representation (2) is unique. Indeed if s are 0. Let us show that the representation (2) is unique. Indeed if
then
But since S is linearly independent, we see that  s - s -  s = 0 for all s. Thus, s = 0 for all s. Thus,  s = s =  s for all s s for all s  S and the representation (2) is unique. Thus, S is a basis of V. S and the representation (2) is unique. Thus, S is a basis of V.
Theorem 5: Let V be a vector space. Then any two bases of V contain the same number of elements.
Proof: Let us consider the special case where V has a finite basis {e1, ..., en}. We will prove that if {fi}i I is any other basis of V, then it is finite and contains n elements. Consideration of the special case suffices, for then if V has one infinite basis, then the special case implies that all bases must be infinite. Since {fi}i I is any other basis of V, then it is finite and contains n elements. Consideration of the special case suffices, for then if V has one infinite basis, then the special case implies that all bases must be infinite. Since {fi}i I is linearly independent, all the fi are nonzero. Let f1 be one of the fi. Since {e1, ..., en} is a basis for V, there exist I is linearly independent, all the fi are nonzero. Let f1 be one of the fi. Since {e1, ..., en} is a basis for V, there exist  1,..., 1,..., n n  F such that F such that
f1 =  e1 e1 + ... +  nen nen.
Since f1 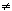 0, not all 0, not all  j are zero. Let us renumber the ej so that j are zero. Let us renumber the ej so that  1 1 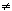 0. Then, since F is a field, 0. Then, since F is a field,
(3)
e1 =  1-1f1 1-1f1 -  1-1 1-1 2e2 2e2 - ... -  1-1 1-1 nen nen.
Let us show that {f1,e2,...,en} is a basis of V. Let v  V. Then there exist V. Then there exist  1,..., 1,...,  F such that F such that
v =  1e1 1e1 + ... +  nen nen.
Therefore, by (3),
v =  1 1' f1 +  2 2' e2 + ... +  n n' fn.
Thus, {f1,e2,...,en} is a set of generators for V. If {f1,e2,...,en} is linearly dependent, then there exist  1,..., 1,..., n n  F such that F such that
(4)
 1f1 1f1 +  2e2 2e2 + ... +  nen nen = 0,
where  1,..., 1,..., n are not all 0. If n are not all 0. If  = 0, then one of = 0, then one of  2,..., 2,..., n is nonzero and n is nonzero and  2e2 + ... + 2e2 + ... +  nen = 0, which contradicts the fact that e2,...,en are linearly independent. Therefore, nen = 0, which contradicts the fact that e2,...,en are linearly independent. Therefore,  1 1 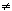 0. Without loss of generality, we may multiply (4) by 0. Without loss of generality, we may multiply (4) by  1-1 and assume that 1-1 and assume that  1 = 1. Then 1 = 1. Then
 1e1 1e1 + (  2 2 +  2 2) e2 + ... + (  n n +  n n) en = 0,  1 1 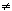 0,
which contradicts the fact that {e1,...,en} are linearly independent. The contradiction proves that {f1,e2...,en} is linearly independent, so that by Proposition 4, {f1,e2...,en} is a basis of V. If n = 1, then {f1} is a basis of V. Therefore, {fi}i I consists of a single element and the theorem is correct. Thus assume the n > 1. If {fi}i I consists of a single element and the theorem is correct. Thus assume the n > 1. If {fi}i I consists only of the single element f1, then {f1} is a basis of V, which contradicts the fact that {f1,e2,...,en} is a basis of V and n > 1. Thus, {fi}i I consists only of the single element f1, then {f1} is a basis of V, which contradicts the fact that {f1,e2,...,en} is a basis of V and n > 1. Thus, {fi}i I consists of at least two elements. Let f2 I consists of at least two elements. Let f2  {fi}i {fi}i I, f2 I, f2 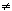 f1. Since {f1,e2,...,en} is a basis of V, there exist f1. Since {f1,e2,...,en} is a basis of V, there exist  1,..., 1,..., n n  F such that F such that
f2 =  1f1 1f1 +  2e2 2e2 + ... +  nen nen,
 1,..., 1,..., n not all 0. If n not all 0. If  2 = ... = 2 = ... =  n = 0, then f1 - n = 0, then f1 -  f1 = 0, which contradicts the fact that f1 and f2 are linearly independent. Thus, one of f1 = 0, which contradicts the fact that f1 and f2 are linearly independent. Thus, one of  1,..., 1,..., n is nonzero. Without loss of generality, assume that n is nonzero. Without loss of generality, assume that  2 2 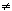 0. Repeating the above argument, we see that {f1,f2,e3...,en} is a basis of V. Continuing in this way, we find f1,...,fn in {fi}i 0. Repeating the above argument, we see that {f1,f2,e3...,en} is a basis of V. Continuing in this way, we find f1,...,fn in {fi}i I such that {f1,...,fn} is a basis of V. But since {fi}i I such that {f1,...,fn} is a basis of V. But since {fi}i I is also a basis for V, we see that {fi}i I is also a basis for V, we see that {fi}i I consists of precisely n elements. For if fn+1 I consists of precisely n elements. For if fn+1  {fi}i {fi}i I is distinct from f1,...,fn, then fn+1 = I is distinct from f1,...,fn, then fn+1 = 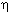 1f1 + 1f1 + 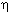 f2 + ... + f2 + ... + 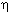 nfn ( nfn (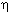 i i  F) since {f1,...fn} is a basis of V. But this contradicts the fact that {f1,...fn+1} are linearly independent. This completes the proof of the theorem. F) since {f1,...fn} is a basis of V. But this contradicts the fact that {f1,...fn+1} are linearly independent. This completes the proof of the theorem.
Remarks: 1. It is possible to strengthen Theorem 5 in case V has infinite dimension. Namely, it is possible to show that not only are any two bases of V is infinite, but given any two bases of V, there exists a bijection of one of these into the other.
2. It is not clear from what we have said that any vector space has a basis. In order to prove this assertion, it is necessary to appeal to Zorn's lemma. If V is finite-dimensional, then the existence of a basis of V was proved. In most of what follows, we will be concerned only with finite-dimensional vector spaces, so we will not give proof of the existence of a basis in the most general case.
|
 V
V V
V
 iei,
iei,  i
i  F.
F.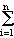
 iei = (
iei = ( 1,
1,  2, ...,
2, ...,  n),
n),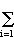
 iei.
iei. v1 + ... +
v1 + ... +  nvn (
nvn ( i
i  F).
F). 2v2 + ... +
2v2 + ... +  nvn,
nvn, 1v1 + ... +
1v1 + ... +  nvn, (
nvn, ( i
i  F)
F) 2 +
2 +  1
1 2)v2 + ... + (
2)v2 + ... + ( n +
n +  1
1 n)vn,
n)vn, 1s1 +
1s1 +  2s2 + ...+
2s2 + ...+  nsn = 0.
nsn = 0. 1s1 +
1s1 +  2s2 + ... +
2s2 + ... +  nsn = 0,
nsn = 0,  i
i  F, si
F, si  S,
S,
 ss,
ss,
 ss,
ss,  s
s  F,
F, (
( s -
s -  s)s.
s)s. e1 + ... +
e1 + ... +  nen.
nen. 1-1f1 -
1-1f1 -  1-1
1-1 2e2 - ... -
2e2 - ... -  1-1
1-1 nen.
nen. 1e1 + ... +
1e1 + ... +  nen.
nen. 1'f1 +
1'f1 +  2'e2 + ... +
2'e2 + ... +  n'fn.
n'fn. 1f1 +
1f1 +  2e2 + ... +
2e2 + ... +  nen = 0,
nen = 0, 1e1 + (
1e1 + ( 2 +
2 +  2)e2 + ... + (
2)e2 + ... + ( n +
n +  n)en = 0,
n)en = 0,  1
1 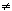 0,
0, 1f1 +
1f1 +  2e2 + ... +
2e2 + ... +  nen,
nen,