|
Arithmetic in a Principal Ideal Domain
We have seen that Z is a unique factorization domain and also a principal ideal domain. On the other hand, Z[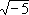 ] is not a unique factorization domain and not a principal ideal domain. Our main result in this section will be the following theorem. ] is not a unique factorization domain and not a principal ideal domain. Our main result in this section will be the following theorem.
Theorem 1: Let R be a principal ideal domain. Then R is a unique factorization domain.
Let us begin by developing the theory of divisibility in an integral domain. Throughout this section, let R be an integral domain. If a,b  R, then we say that a divides b (denoted a|b) if b = xa for some x R, then we say that a divides b (denoted a|b) if b = xa for some x  R. If a does not divide b, we write a R. If a does not divide b, we write a  b. The elementary facts about divisibility are summarized in the following result: b. The elementary facts about divisibility are summarized in the following result:
Lemma 2: Let a,b,c  R. Then: R. Then:
(1) a|b, b|c  a|c. a|c.
(2) a|b  a|bc for all c a|bc for all c  R. R.
(3) a|b, a|c  a|b+c. a|b+c.
(4) a|b, a|c  a|bx + cy for all x,y a|bx + cy for all x,y  R. R.
(5) Let b 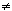 0. Then a|b, b|a 0. Then a|b, b|a  a and b are associates. a and b are associates.
Proof:
(1) b = xa, c = yb  c =(xy)a c =(xy)a  a|c. a|c.
(2) b = xa  bc = (xc)a bc = (xc)a  a|bc. a|bc.
(3) b = xa, c = ya  b + c = (x + y)a b + c = (x + y)a a|b + c. a|b + c.
(4) By (ii) and (iii), a|bx, a|cy  a|bx + cy. a|bx + cy.
(5) b = xa, a = yb  b = (xy)b b = (xy)b  b(1-xy) = 0 b(1-xy) = 0  1-xy = 0 since b 1-xy = 0 since b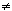 0 and since R is an integral domain 0 and since R is an integral domain  xy = 1 xy = 1  x is a unit of R x is a unit of R  a a b are associates since b = xa. a a b are associates since b = xa.
It is possible to formulate the notion of divisibility in terms of ideals. For if a|b, then b = xa  b b  (a) (a)  by by  (a) for all y (a) for all y  R R  (b) (b) 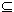 (a). Conversely, if (b) (a). Conversely, if (b) 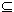 (a), then b (a), then b  (a), so that b = xa and a|b. Thus we have (a), so that b = xa and a|b. Thus we have
(1)
a|b if and only if (b) 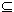 (a).
Lemma 3: Let a,b  R. Then a and b are associates if and only if (a) = (b). R. Then a and b are associates if and only if (a) = (b).
Proof:  If a and b are associates, a = If a and b are associates, a =  b, where b, where  is a unit of R. Therefore, b = is a unit of R. Therefore, b =  -1a, so that b|a and a|b. Thus by (1), -1a, so that b|a and a|b. Thus by (1),
(a) 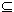 (b), (b) 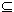 (a).
 (a) = (b).
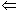 Suppose that (a) = (b). Then by (1), we have a|b and b|a, so that a and b are associates by Lemma 2,part(5). Suppose that (a) = (b). Then by (1), we have a|b and b|a, so that a and b are associates by Lemma 2,part(5).
Definition 4: Let a,b  R. A greatest common divisor (g.c.d) of a and b is an element c of R having the following properties: R. A greatest common divisor (g.c.d) of a and b is an element c of R having the following properties:
(1) c|a, c|b.
(2) If d  R is such that d|a and d|b, then d|c. R is such that d|a and d|b, then d|c.
In the case R = Z, Definition 4 is essentially the same as the definition of g.c.d. that was given in the section on integers. There is one small difference, however. Earlier, we required that a g.c.d. be positive. In a general ring, the notion of positivity makes no sense, and therefore we cannot include the condition of positivity in Definition 4. Therefore, if a = 3, b = 6, then (a,b) = 3 using the earlier definition, whereas both 3 and -3 are g.c.d's in the sense of Definition 4. Note that 3 and -3 are associates. This is not an accident.
Lemma 5: Let a,b  R, and let c and c' be two g.c.d.'s of a and b. Then c and c' are associates. R, and let c and c' be two g.c.d.'s of a and b. Then c and c' are associates.
Proof: Since c|a and c|b, and since c' is a g.c.d. condition (2) of Definition 4 implies that c|c'. Reversing the roles of c and c', we see that c'|c. If c = 0, then c' = 0 and the lemma holds. If c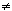 0, then Lemma 2, part (5) implies that c and c' are associates. 0, then Lemma 2, part (5) implies that c and c' are associates.
Thus, we see that if c0 is a g.c.d. of a and b, then all g.c.d's of a and b are of the form  c0, where c0, where  is a unit of R. is a unit of R.
Definition 6: Let a,b  R. We say that a and b are relatively prime, denoted (a,b) = 1, if 1 is a g.c.d of a and b. R. We say that a and b are relatively prime, denoted (a,b) = 1, if 1 is a g.c.d of a and b.
In an arbitrary integral domain R, it is not usually true that every pair of elements a,b  R have a g.c.d. However, if R is a PID, then no pathologies occur and g.c.d's exist. R have a g.c.d. However, if R is a PID, then no pathologies occur and g.c.d's exist.
Proposition 7: Let R be a principal ideal domain and let a,b  R, a and b not both 0. Then a and b have a g.c.d in R. R, a and b not both 0. Then a and b have a g.c.d in R.
Proof: Let I = (a,b). Since R is a PID, I = (c) for some c  R. Moreover, since a and b are not both 0, I R. Moreover, since a and b are not both 0, I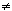 (0), so that c (0), so that c 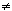 0. Let us show that c is a g.c.d. of a and b. Since a,b 0. Let us show that c is a g.c.d. of a and b. Since a,b  I, we see that a = cx, b = cy I, we see that a = cx, b = cy c|a, c|b c|a, c|b  (1). Suppose d (1). Suppose d  R such that d|a and d|b. Since I = (a,b) = {ax + by | x,y R such that d|a and d|b. Since I = (a,b) = {ax + by | x,y  R}, we have c = ax + by for some x,y R}, we have c = ax + by for some x,y  R. But then by Lemma 2 part (4), we have d|ax+by R. But then by Lemma 2 part (4), we have d|ax+by  d|c. d|c.
Corollary 8: Let R be a PID, and let a,b  R, a, b not both 0. Then every g.c.d of a and b can be written in the form ax + by for some x,y R, a, b not both 0. Then every g.c.d of a and b can be written in the form ax + by for some x,y  R. In particular, if a and p are relatively prime, then there exist x,y R. In particular, if a and p are relatively prime, then there exist x,y  R such that ax + by = 1. R such that ax + by = 1.
In the case of integers, we proved that if p is prime and a and b are integers such that p|ab, then either p|a or p|b. Let us generalize this result to a PID.
Theorem 9: Let R be a principal ideal domain and let a,b  R. Let R. Let  be an irreducible element of R such that be an irreducible element of R such that  |ab. Then either |ab. Then either  |a or |a or  |b. |b.
Proof: Let us assume that  does not divide a. We must then show that does not divide a. We must then show that  |b. Since |b. Since  is irreducible, is irreducible,  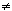 0 and thus 0 and thus  and a must have a g.c.d and a must have a g.c.d  by Proposition 7. But by Proposition 7. But  | | so that so that  is either an associate of is either an associate of  or a unit of R. In the former case, or a unit of R. In the former case,  |a since |a since  |a. And this contradicts our assumption. Therefore, |a. And this contradicts our assumption. Therefore,  is a unit of R and is a unit of R and   -1 is a g.c.d of -1 is a g.c.d of  and a, since and a, since  -1 is a unit of R. But then by Corollary 8, there exist x,y -1 is a unit of R. But then by Corollary 8, there exist x,y  R such that R such that
 x + ay = 1.
Thus we see that  (bx) + (ab)y = b. However (bx) + (ab)y = b. However  | | and and  |ab. so that by Lemma 2, part(4), we see that |ab. so that by Lemma 2, part(4), we see that  | | bx + aby so that bx + aby so that  |b. |b.
Corollary 10: Let R be a PID, a1,...,an  R, R,  and irreducible element of R. If and irreducible element of R. If  |a1··· an, then |a1··· an, then  |ai for some i. |ai for some i.
We now come the the proof of Theorem 1. Our proof will be divided into two parts. First we will show that if x  Rx, x Rx, x  UR, then x can be written as a product of irreducible elements. Second, we will show that the expression of x a product of irreducible elements is unique up to order and multiplication of the irreducible elements by units. UR, then x can be written as a product of irreducible elements. Second, we will show that the expression of x a product of irreducible elements is unique up to order and multiplication of the irreducible elements by units.
Theorem 11: Let x  Rx, x Rx, x  UR. Then x can be written as a product of irreducible elements. UR. Then x can be written as a product of irreducible elements.
Proof: Let us reason by contradiction. Assume that x cannot be written a product of irreducible elements. In particular, x is not irreducible, so that we may write
x = a 1b 1, a 1,b 2 not units.
Either a1 of b1 cannot be written as irreducible elements. For otherwise, x could be so written. Thus suppose that a1 is not a product of irreducible elements. Since x = a1b1, we see that a1|x and thus (a1)  (x) by (1). Moreover, since b1 is not a unit, (a1) (x) by (1). Moreover, since b1 is not a unit, (a1)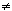 (x) by Lemma 3. Thus, (x) is not properly contained in (a1). Let us denote this fact by (a1) (x) by Lemma 3. Thus, (x) is not properly contained in (a1). Let us denote this fact by (a1)  (x). Note that a1 (x). Note that a1  Rx, a1 Rx, a1  UR, and a1 cannot be written as a product of irreducible elements. Thus we can apply the same reasoning to a1 as we did to x to find a2 UR, and a1 cannot be written as a product of irreducible elements. Thus we can apply the same reasoning to a1 as we did to x to find a2  Rx, a2 Rx, a2  UR, a2 not equal to a product of irreducible elements, and (a2) UR, a2 not equal to a product of irreducible elements, and (a2)  (a1). Let us proceed in this way and construct a3,a4, a5,.... We eventually arrive at the following chain of ideals (a1). Let us proceed in this way and construct a3,a4, a5,.... We eventually arrive at the following chain of ideals
(2)
where a0 = x. Set
(3)
I = 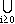 (a i).
Let us prove that I is an ideal of R. Let a,b  I. Then a I. Then a  (ai), b (ai), b  (aj) for some i and j. Let j > i. Then (ai) (aj) for some i and j. Let j > i. Then (ai) 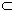 (aj) and a,b (aj) and a,b  (aj). But since (aj) is an ideal a±b (aj). But since (aj) is an ideal a±b  (aj), so that a±b (aj), so that a±b  I. Thus I is an additive subgroup of R. A similar argument shows that I is closed with respect to multiplication by elements of R. This shows that I is an ideal of R. Since R is a PID, I = (a) for some a I. Thus I is an additive subgroup of R. A similar argument shows that I is closed with respect to multiplication by elements of R. This shows that I is an ideal of R. Since R is a PID, I = (a) for some a  R. Now a R. Now a  I, so that a I, so that a  (ak) for some k. Therefore, (a) (ak) for some k. Therefore, (a) 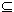 (ak). However, (ak) (ak). However, (ak)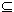 I = (a), so that (a) = (ak). In particular, (ak+1) I = (a), so that (a) = (ak). In particular, (ak+1) 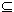 (ak) by (3). But this is a contradiction to (2), which asserts that (ak) (ak) by (3). But this is a contradiction to (2), which asserts that (ak)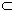 (ak+1). (ak+1).
Theorem 12: Let x  Rx, x Rx, x  UR and let UR and let
be two expressions of x as a product of irreducible elements. Then s = t and by renumbering  1,..., 1,..., s, we can guarantee that s, we can guarantee that  i and i and  i are associates (1 < i < s). i are associates (1 < i < s).
Proof: If s = 1, then x is irreducible and the assertion is clear. Assume that s > 1 and let us proceed by induction on s. Since  1|x, we see that 1|x, we see that  | | 1... 1... t. Therefore, by Corollary 10, t. Therefore, by Corollary 10,  1| 1| i for some i (1 < i < t). by renumbering i for some i (1 < i < t). by renumbering  1,..., 1,..., t, we may assume that i = 1, so that t, we may assume that i = 1, so that  1| 1| 1. But since 1. But since  1 is irreducible and 1 is irreducible and  1 is not a unit we see that 1 is not a unit we see that  1 and 1 and  1 are associates, say 1 are associates, say   1 = 1 =  1, 1,   UR. Therefore, UR. Therefore,
Set  2' = 2' =   2, 2,  3' = 3' =   3,,..., 3,,..., t' = t' =   t. Then t. Then  i' and i' and  i are associates and i are associates and  2... 2... s = s =  2... 2... t' are two decompositions of t' are two decompositions of  2... 2... s into irreducible factors. Therefore by the induction hypothesis, s - 1 = t - 1 and after renumbering s into irreducible factors. Therefore by the induction hypothesis, s - 1 = t - 1 and after renumbering  2'... 2'... t', we can guarantee t', we can guarantee  i and i and  i' are associates (2 < i < s). But then s = t and i' are associates (2 < i < s). But then s = t and  i and i and  i are associates (1 < i < s). Thus the induction step is established. i are associates (1 < i < s). Thus the induction step is established.
We showed in the previous section that if F is a field and X is an indeterminate over F, then F[X] is a PID. Therefore by Theorem 1, we see that F[X] is a UFD. Let us see exactly what this says: The units of F[X] are just the nonzero constant polynomials. Therefore f  F[X] is a nonzero, nonconstant polynomial, then f can be written in the form F[X] is a nonzero, nonconstant polynomial, then f can be written in the form
(4)
f = f1...ft,
where fi  F[X] is an irreducible polynomial. Moreover, the decomposition (4) is unique up to a rearrangement and multiplication of the fi by constants. Let f = anXn + an-1Xn-1 + ... + a0, an F[X] is an irreducible polynomial. Moreover, the decomposition (4) is unique up to a rearrangement and multiplication of the fi by constants. Let f = anXn + an-1Xn-1 + ... + a0, an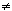 0> Then an is called the leading coefficient of f. If f has a leading coefficient 1, then we say that f is monic. It is clear that a nonzero polynomial g = bmXm + ... + b0, bm 0> Then an is called the leading coefficient of f. If f has a leading coefficient 1, then we say that f is monic. It is clear that a nonzero polynomial g = bmXm + ... + b0, bm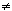 0 can be written as the product of a constant and a monic polynomial: 0 can be written as the product of a constant and a monic polynomial:
g = bm(Xm + bm-1bm-1Xm-1+...+bm-1b0).
Therefore we can write
(5)
f = af1*...ft*,
where a is a constant and fi* is monic and irreducible. By comparing leading coefficients on both sides of (5), we see that a = an.
Proposition 13: Let F be a field, X an indeterminate over F, f a nonzero, nonconstant polynomial in F[X], a the leading coefficient of f. Then f can be written in the form
f = af1*...ft*,
where fi* is an irreducible, monic polynomial. Moreover, this decomposition is unique up to the order of the fi*.
Proof: All that must be proved is the uniqueness. Let
f = af1*...ft* = ag1*...gs*,
be two decompositions of f, where fi* and gi* are irreducible and monic. Since F[X] is a UFD, we have s = t and may renumber f1*,...ft* so that fi* and gi* are associates (1 < i < s). But since fi* and gi* are both monic, fi* = gi*.
|
 R.
R. y
y of R.
of R.
 R.
R. y
y of R.
A ring R having the property that every ideal is principal is called a principal ideal ring (PIR). If, in addition, R is an integral domain, then R is called a principal ideal domain (PID).
We say that R is a unique factorization domain if the following two conditions are satisfied: (1) If
of R.
A ring R having the property that every ideal is principal is called a principal ideal ring (PIR). If, in addition, R is an integral domain, then R is called a principal ideal domain (PID).
We say that R is a unique factorization domain if the following two conditions are satisfied: (1) If  Rx
Rx Rx
Rx 1 ...
1 ...  s =
s =  1 ...
1 ...  t
t 1 ...
1 ...  s
s 1 and
1 and  1 are associates
1 are associates  R.
R.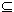 (a).
(a).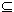 (b), (b)
(b), (b) 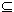 (a).
(a). (a) = (b).
(a) = (b). x + ay = 1.
x + ay = 1.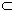 (a1)
(a1) 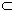 (a2)
(a2) 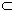 ...,
..., (ai).
(ai). 1...
1... s =
s =  1...
1... t
t 1...
1... s =
s = 
 1
1 2...
2... t,
t, 1(
1( 2...
2... s-
s-
 2...
2... t) = 0,
t) = 0,