 I,
I, R,
R, I
I I.
I.
 I,
I, R,
R, I
I I.
The set of integers.
If
I.
The set of integers.
If 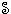 is any nonempty collection of subgroups of the group G, then the intersection H* =
is any nonempty collection of subgroups of the group G, then the intersection H* = 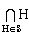 is a subgroup of G.
is a subgroup of G.
| Back | Table of Contents |
|
|
The Arithmetic of IdealsLet R be a commutative ring with identity. In this section we will begin to study the arithmetic of ideals in R.
Lemma 1: Let
A =
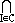 I Iis an ideal of R. Proof: From Theorem 3 of the section on subgroups, we know that A is a subgroup of the additive group of R. Let Let S be a subset of R. Then there exists a smallest ideal of R which contains S. Let
A =
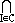 I I
is an idea of R by Lemma 1 and it is clear that A contains S. Furthermore, if A0 is a ideal of R which contains S, then If
Proposition 2: Let
r1s1 + r2s2 + ... + rtst (ri
 R, si R, si  S). S).Proof: It is clear that every sum of the form (1) belongs to I, since I is an ideal containing S. Therefore, it suffices to show that the set of sums (1) form an ideal containing S, since I is the smallest such ideal. Since the elements of (1) will form a ring. That is an ideal, if there is another element t that is not in the form of (1) it would contradict the fact that (S) is the smallest ideal.
Corollary 3: Let
r1a1 + ... + rnan (ri
 R). R).Example 1: Let R be arbitrary. Then (0) is the ideal consisting of only 0, and (1) contains Example 2: Let
x = q · a + r, 0 < r < a.
Since Example 3: Let F be a field. Then (0) and (1) are ideals of F. Let Example 4: Let F be a field, X an indeterminate over F,
h = q · g + r, deg(r) < deg(g).
Since Example 5: Let us give an example of a ring in which not every ideal is principal. Let F be a field and let X and Y be indeterminates over F. Let us consider the ideal A ring R having the property that every ideal is principal is called a principal ideal ring (PIR). If, in addition, R is an integral domain, then R is called a principal ideal domain (PID). For example, Z, a field F, a polynomial ring Let A and B be ideals of R. The sum A + B of A and B is the ideal generated by
r1a1 + ... + rn + s1b1 + ... + smbm,
(ri, sj
 R, ai R, ai  A, bj A, bj  B). B).
But since A and B are ideals,
A + B = {a + b | a
 A, b A, b  B}. B}.
For example, if
(2) + (4) = {2m + 4n | m,n
 Z} Z}
= {2k | k
 Z} Z}
= (2);
(5) + (7) = {5m + 7n | m,n
 Z} Z}
= (1),
since
(a) + (b) = {am + bn | m,n
 Z}. Z}.
If
(a) + (b) =(c),
where c is the smallest positive integer contained in
Lemma 4: Let
(a) + (b) = ((a,b)).
By Lemma 4, it is reasonable to regard the sum of two ideals (a), (b) of a general ring R as some sort of greatest common divisor of a and b. This was Kummer's great idea. Define the g.c.d. of two elements Let A and B be ideals of R. The product
a1 · b1 + ... + an · bn, ai
 A, bj A, bj  B. B.It is easy to see that (2)
(a) · (b) = (a · b),
(a1,...,am)·(b1,...,bn)=
(3)
(a1 · b1,a1 · b2,...,a1 · bn,a2b1,...,am · bn).
Thus, for example, in
(X,Y) · (X2,Y) = (X3, XY, X2Y, Y2).
The following are properties of sums and products of ideals which can easily be proven. Let A,B and C be ideals of R. Then (4)
A + B = B + A,
(5)
A + (B + C) = (A + B) + C,
(6)
A · B = B · A,
(7)
A · (B · C) = (A · B) · C,
(8)
A · (B + C) = A · B + A · C.
One surprising property of the product is (9)
A · B
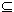 A A  B. B. |
| Back | Table of Contents |