|
Factorization of Polynomials in Q[X]
Since Q[X] is a UFD, every nonconstant polynomial f  Q[X] can be factored into a product of irreducible polynomials. This is guaranteed by our general theory. However, our general theory provides us with no way which this factorization can be carried out in particular cases. No doubt, the reader has factored many polynomials in elementary algebra. However, the methods used there are usually ad hoc, depending on a series of tricks. Moreover, these methods provide no real insight into the reducibility or irreducibility of a given polynomial. Q[X] can be factored into a product of irreducible polynomials. This is guaranteed by our general theory. However, our general theory provides us with no way which this factorization can be carried out in particular cases. No doubt, the reader has factored many polynomials in elementary algebra. However, the methods used there are usually ad hoc, depending on a series of tricks. Moreover, these methods provide no real insight into the reducibility or irreducibility of a given polynomial.
In this section we will use the theory we have developed in order to provide a computational procedure for factoring polynomials in Q[X], This beautiful development is due to the German Mathematician Kronecker. Kronecker believed that mathematics should concern itself only with objects which can be computed or constructed in a finite number of steps. Thus, for Kronecker, a proof which asserts the existence of a mathematical object, without prescribing a recipe for constructing the object in a finite number of steps, is no proof at all. The developments of this section are very much in the spirit of Kronecker's philosophy.
First, let us make a few observations concerning polynomials. Let F be a field and let  1,..., 1,..., n+1, n+1, 1,..., 1,..., n+1 be elements of F with n+1 be elements of F with  1,..., 1,..., n+1 distinct. The Lagrange interpolation formula allows us to construct a polynomial f n+1 distinct. The Lagrange interpolation formula allows us to construct a polynomial f  F[X] of degree at most n such that F[X] of degree at most n such that
(1)
f(  i i) =  i i (1 < i < n + 1).
In fact, a polynomial f which works is given by
(2)
Lemma 1: Let f  F[X], F[X],   F. if f( F. if f( ) = 0, then X - ) = 0, then X -  | f. Thus, if deg(f) = n and f has more than n zeros in F, then f = 0. | f. Thus, if deg(f) = n and f has more than n zeros in F, then f = 0.
Proof: By the division algorithm in F[X], there exist polynomials g and r such that
(3)
f = g(X -  ) + r, deg(r) < deg(X -  ) = 1.
Setting X =  in (3), we see that r( in (3), we see that r( ) = 0. But since deg(r) < 0, r is a constant polynomial and r = 0. Thus, f = g(X - ) = 0. But since deg(r) < 0, r is a constant polynomial and r = 0. Thus, f = g(X -  ) and X - ) and X -  |f. If deg(f) = n and f has zeros |f. If deg(f) = n and f has zeros  1,..., 1,..., n+1 in F, then X - n+1 in F, then X -  i|f (1 < i < n+1), so that (X - i|f (1 < i < n+1), so that (X -  1)···(X - 1)···(X -  n+1)|f. Therefore, f = 0. n+1)|f. Therefore, f = 0.
Proposition 2: Let  1,..., 1,..., n+1, n+1, 1,... 1,... n+1 n+1  F with F with  1,..., 1,..., n+1 distinct. Then there exists one and only one polynomial f n+1 distinct. Then there exists one and only one polynomial f  F[X] such that deg(f) < n and f( F[X] such that deg(f) < n and f( i) = i) =  i (1 < i < n + 1). i (1 < i < n + 1).
Proof: The existence of f is guaranteed by (2). Suppose that f and f * satisfy the conditions of the proposition. Then deg(f - f *) < n and f - f * has the n + 1 zeros  1,... 1,... n+1. Therefore by Lemma 1, f - f * = 0. n+1. Therefore by Lemma 1, f - f * = 0.
Now let us describe Kronecker's factorization algorithm. Without loss of generality, let us restrict ourselves to consideration of a nonconstant primitive polynomial f  Z[X] of degree n. Then the irreducible factors of f in Q[X] can be taken to be primitive polynomials in Z[X]. If f is not irreducible in Z[X], then f has a factor of degree < n/2. Thus in order to factor f, it suffices to determine whether f is irreducible and, if it is not, to find a factor of f of degree < n/2. For in the latter case, we can write Z[X] of degree n. Then the irreducible factors of f in Q[X] can be taken to be primitive polynomials in Z[X]. If f is not irreducible in Z[X], then f has a factor of degree < n/2. Thus in order to factor f, it suffices to determine whether f is irreducible and, if it is not, to find a factor of f of degree < n/2. For in the latter case, we can write
f = gh, deg(g) < n/2, g,h  Z Z[X],
and then we can repeat the procedure to determine whether g or h is irreducible. Eventually, we will get a factorization of f into primitive, irreducible polynomials in Z[X].
Suppose that s = the largest positive integer < m/2, and suppose that g is a factor of f in Z[X], deg(g) < n/2. Then for any integer  , g( , g( )|f( )|f( ). In particular, if f( ). In particular, if f( ) )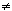 0, then g( 0, then g( ) is a divisor of f( ) is a divisor of f( ) and there are only finitely many choices for g( ) and there are only finitely many choices for g( ). Since f has at most n zeros in Z, among the integers 1,2,3,...,2n, we may select s + 1 of them, say ). Since f has at most n zeros in Z, among the integers 1,2,3,...,2n, we may select s + 1 of them, say  0,..., 0,..., s, such that f( s, such that f( i) i)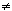 0 (0 < i < s). For each 0 (0 < i < s). For each  i let us compute S( i let us compute S( i) = the set of divisors of f( i) = the set of divisors of f( i). Then by our observations above g( i). Then by our observations above g( i) i)  S( S( i), deg(g) < s. Moreover, if i), deg(g) < s. Moreover, if  0 0  S( S( 0), 0),  1 1  S( S( 1),..., 1),..., z z  S( S( s), then there exists one and only one g such that deg(g) < s and g( s), then there exists one and only one g such that deg(g) < s and g( i = i =  i (0 < i < s), and this particular g can be calculated using (2).Thus our plan of calculation is clear. For each (s+1)-tuple ( i (0 < i < s), and this particular g can be calculated using (2).Thus our plan of calculation is clear. For each (s+1)-tuple ( 0,..., 0,..., s), s),  i i  S( S( i), we construct a unique g given by (2). Then using long division, we determine whether g is a factor of f. If none of the factors so constructed work, then f is irreducible. i), we construct a unique g given by (2). Then using long division, we determine whether g is a factor of f. If none of the factors so constructed work, then f is irreducible.
This algorithm is rather clumsy to carry out manually, but it is rather easy to program. Nevertheless, let us carry out an easy example. Let f = X3 - 3X2 + 4X + 1. Then s = 1, and since f(0) = 1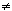 0, f(1) = 3 0, f(1) = 3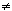 0, we may set 0, we may set  1 = 0, 1 = 0,  2 = 1. Then S( 2 = 1. Then S( 1) = {1,-1}, S( 1) = {1,-1}, S( 2) = {3,-3,1,-1}. Note that if g corresponds to ( 2) = {3,-3,1,-1}. Note that if g corresponds to ( 1, 1, 2), then -g corresponds to (- 2), then -g corresponds to (- 1,- 1,- 2), so that is enough to check the cases 2), so that is enough to check the cases
(  1 1,  2 2 = (1,3), (1,-3), (1,1), (1,-1).
In these cases, the value of g is respectively
2X + 1, 4X + 1, 1, -2X + 1.
However, none of these is a factor of f, so f is irreducible.
Kronecker's algorithm proceeds much more quickly if we can recognize irreducible polynomials easily. A simple test for irreducibility which is often applicable is the Eisenstein irreducibility criterion.(Eisenstein was a pupil of Gauss).
Theorem 3 (Eisenstein): Let f = a0+a1X+...+anXn  Z[X] be primitive and let p be prime. Assume that p|ai (0 < i < n-1), p Z[X] be primitive and let p be prime. Assume that p|ai (0 < i < n-1), p an, p2 an, p2 a0. Then f is irreducible in Z[X]. a0. Then f is irreducible in Z[X].
Proof: Let us reason by contradiction. Assume that
f = (b 0 + ... + b tX t)(c 0+... + c uX u); b i,c i Z Z,
where t > 1, u > 1. Since a0 = b0c0 and since p2 a0, we see that p cannot divide both of b0 and c0. On the other hand, since p|a0, p divides one of b0,c0. Assume that p a0, we see that p cannot divide both of b0 and c0. On the other hand, since p|a0, p divides one of b0,c0. Assume that p b0 and p|c. Since f is primitive, not all ci are divisible by p. Let cv be the first ci which is not divisible by p. Then, b0 and p|c. Since f is primitive, not all ci are divisible by p. Let cv be the first ci which is not divisible by p. Then,
av = bvc0 + bv-1c1 + ... + b0cv.
By assumption, p|av. Moreover, p|c0, p|c1,...,p|cv-1 by the choice of v. Therefore, p|b0cv, which contradicts the facts p cv, p cv, p b0. b0.
Example 1: X3 + 3X2 + 9X + 6 is irreducible in Z[X]. (set p = 3). f(X + 1) = X4 + X3 + X2 + X + 1 is irreducible in F[X]. Indeed since
f(X + 1) = X4 + 5X3 + 10X2 + 10X + 5,
we see that f(X + 1) is irreducible in Z[X]. Thus f is irreducible in Z[X].
|
 Rx
Rx Rx
Rx 1 ...
1 ...  s =
s =  1 ...
1 ...  t
t 1 ...
1 ...  s
s 1 and
1 and  1 are associates
1 are associates  Rx
Rx Rx
Rx 1 ...
1 ...  s =
s =  1 ...
1 ...  t
t 1 ...
1 ...  s
s 1 and
1 and  1 are associates
1 are associates  R,
R, i) =
i) =  i (1 < i < n + 1).
i (1 < i < n + 1).
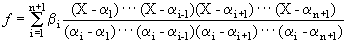
 ) + r, deg(r) < deg(X -
) + r, deg(r) < deg(X -  ) = 1.
) = 1. Z[X],
Z[X], 1,
1, 2 = (1,3), (1,-3), (1,1), (1,-1).
2 = (1,3), (1,-3), (1,1), (1,-1). Z,
Z,