Euclidean Domains
In the previous section we proved that a principal ideal domain possesses the property of unique factorization. Now we are faced with the problem of determining whether or not a given integral domain is a principal ideal domain. This is generally a very difficult question. However, a partial solution is available. Notice that we were able to prove that Z and
Definition 1: Let R be an integral domain. Then R is called a Euclidean domain if there exists a function  :R
:R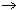 Z
Z
(1)  (x) > 0
(x) > 0 R.
R.
(2)  (x) = 0
(x) = 0
(3)  (xy) =
(xy) =  (x)
(x) (y)
(y) R.
R.
(4) Let  R,
R,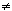 0.
0. R
R (r) <
(r) <  (y).
(y).
Example 1: Let  (x) = |x|.
(x) = |x|.
Example 2: Let  (x) = 2deg(x)
(x) = 2deg(x)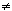 0), and
0), and  R,
R,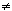 0,
0, R
R (r) <
(r) <  (y)
(y)
Theorem 2: Let R be a Euclidean domain. Then R is a principal ideal domain.
Proof: Let I be a nonzero ideal of R. It suffices to show that I is principal. Let  I
I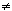 0 and
0 and  (a)
(a)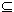 I.
I. I.
I. R
R
 (r) <
(r) <  (a).
(a).
Note that  I
I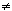 0,
0, (r) <
(r) <  (a),
(a), I,
I, (a).
(a).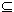 (a).
(a).
Let us now give an example of a Euclidean domain which is connected with Fermat's last theorem.
Theorem 3: Let  = (-1 +
= (-1 + 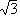 i)/2.
i)/2. is a primitive cube root of 1 and
is a primitive cube root of 1 and  ]
]
Before proving Theorem 3, it is necessary to describe  ]
] 2 +
2 +  + 1 = 0,
+ 1 = 0,
Also,  3 = -
3 = - 2 -
2 -  ,
,
Proceeding by induction, we see that
for all
Moreover, every element of  ]
] ,
,
 = a' + b'
= a' + b'
 a - a' = (b' - b)
a - a' = (b' - b)
 b' - b = 0
b' - b = 0 a - a' =0.
a - a' =0.And we have proved the following
Lemma 4: Every element of  ]
] ,
, Z.
Z.
Proof of Theorem 3: If  Q,
Q, (a + b
(a + b ) =
) = )(a + b
)(a + b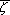 ) =
) =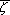 denotes the complex conjugate of
denotes the complex conjugate of  . Since
. Since 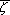 = a + b
= a + b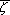 ,
, (a + b
(a + b ) =
) = |2 > 0.
|2 > 0. (a + b
(a + b ) = 0
) = 0 
 = 0.
= 0. Z,
Z, (a + b
(a + b ) =
) = Z.
Z. (
(
 ) =
) =  (
( )
) (
( )
) ,
,
 {a + b
{a + b | a,b
| a,b  Q}.
Q}. . Let
. Let  ,
,
 Z[
Z[ ],
],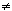 0.
0.

where
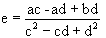 ,
, 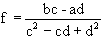
belong to Q. There exist integers  and
and  such that
such that
 | < 1/2, |f -
| < 1/2, |f -  | < 1/2.
| < 1/2.
Set  +
+ 
 ,
, ) + (f -
) + (f -  )
) ]y.
]y. Z[
Z[ ]
]
so that  Z[
Z[ ].
].
 (r) =
(r) =  ((e -
((e -  ) + (f -
) + (f -  )
) )
) (y)
(y) )2 - (e -
)2 - (e -  )(f -
)(f -  ) + (f -
) + (f -  )2}
)2} (y)
(y) (y)
(y) (y).
(y).
Corollary 5: If  = (-1 +
= (-1 + 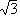 i)/2
i)/2 ]
]