Sets
In mathematics, one naturally meets with collections of various kinds of objects. For example, the collection of all points on a line, the collection of all positive integers less than 100, the collection of all lines passing through a given point of the plane, are all collections which arise naturally in elementary mathematics. These collections are typical examples of sets. Roughly speaking, a set is any well-defined collection of objects. When we say "well-defined", we mean that it is possible to tell, without ambiguity, whether or not a given object belongs to the set. The reason we have defined the notion of a set only 'roughly' is that in more formal developments of set theory, "set" is an undefined term, whose properties are described by a system of axioms. Thus, the notion of "set" in set theory is analogous to the notions of "point" and "line" in Euclidean geometry.
Cantor was certainly not the first mathematician to use sets. Sets had come up in connection with particular mathematical problems centuries before Cantor. But it was Cantor who first considered the properties of general sets in a systematic way. And to understand the impact of the theory of sets on mathematics, it is necessary to consider the state of mathematics in the early nineteenth century. The Greek concept of mathematics as a deductive science was firmly entrenched. But the axioms from which mathematicians deduced their results were never quite spelled out. For example, mathematicians worked incessantly with real numbers, without ever knowing precisely what a real number was. One of the great triumphs of Cantor was to give a definition of a real number in terms of sets, which could be described by a rather simple list of properties. It is precisely the simplicity and generality of the notion of a set which makes it so natural a concept on which to lay the foundations of mathematics.
An object belonging to a set A is called an element of A. If x is an element of A then we write  A
A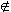 A.
A. B.
B.
Sets:Proposition 1: Let A and B be sets. If  B
B A.
A. B
B A,
A,
Let A and B be sets. If  B
B A.
A. B
B A,
A,
Proof: If  B
B A.
A. B
B A,
A,
Proposition 1 is extremely useful, because it gives a convenient way of proving that two sets A and B are equal by proving that  B
B A.
A.
If A is a set, we will often display the elements of a set by inserting them in braces. Thus, if A is the set consisting of the first five letters of the English alphabet, then we write  A,
A, A | P(x)}.
A | P(x)}.
 B | x is even}={0,2,4,...}.
B | x is even}={0,2,4,...}. The set which contains no elements will bet call the null set (or empty set) and will be denoted by 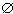 . Note that
. Note that 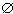 is a subset of every set A, because every element of
is a subset of every set A, because every element of 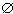 is contained in A.
is contained in A.
Let 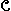 be a collection of sets that is, let
be a collection of sets that is, let 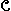 be a set (always assumed to be nonempty) whose elements are sets A, B, C,....It does not matter for the present whether the number of sets in
be a set (always assumed to be nonempty) whose elements are sets A, B, C,....It does not matter for the present whether the number of sets in 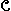 is finite. The union of the collection
is finite. The union of the collection 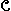 is the set whose elements are those elements which belong to at least one set of the collection
is the set whose elements are those elements which belong to at least one set of the collection 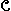 . The intersection of the collection is the set whose elements are those elements which belong to every set of the collection
. The intersection of the collection is the set whose elements are those elements which belong to every set of the collection 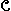 . The union and intersection of the collection
. The union and intersection of the collection 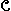 are denoted
are denoted

and
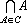
respectively. If 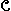 consists of a finite number of sets, say
consists of a finite number of sets, say
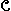 ={A1,...An},
={A1,...An},
then we will denote the union and intersection of
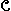 by
by
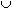 ...
...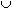 An
Anand
 ...
... An,
An,respectively.
Let us consider a few examples of the above definitions. Let R denote the set of all real numbers and define C1,C2, and C3 by
 R | 0<x<1}
R | 0<x<1}C2={x
 R | 0<x<3},
R | 0<x<3},C3={x
 R | -1<x<½}
R | -1<x<½}Then
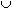 C2
C2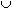 C3={x
C3={x R | -1<x<3},
R | -1<x<3},C1
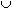 C2={x
C2={x R | 0<x<3},
R | 0<x<3},C1
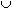 C3={x
C3={x R | -1<x<1},
R | -1<x<1},C1
 C2
C2 C3={x
C3={x R | 0<x<½},
R | 0<x<½},C1
 C2={x
C2={x R | 0<x<1}
R | 0<x<1}Let A and B be sets. Then the set  A | x
A | x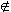 B}
B}
Thus, using the same sets C1,C2, and C3 as above, we can immediately see that
 R | ½<x<1},
R | ½<x<1},C1-C2={0},
C2-C3={x
 R | ½<x<3}
R | ½<x<3}There are a number of elementary properties of unions, intersections, and differences which are very useful in manipulating with sets. Let A, B, and C be sets. Then
(1)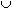 (B
(B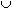 C)=
(A
C)=
(A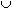 B)
B)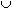 C,
C,
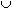 B=B
B=B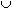 A,
A,
 (B
(B C)=
(A
C)=
(A B)
B) C,
C,
 B=B
B=B A,
A,
 C)=(A-B)
C)=(A-B)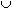 (A-C),
(A-C),
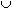 C)=(A-B)
C)=(A-B) (A-C).
(A-C).
Formulas (5) and (6) are called
de_Morgan's formulas. All of the above formulas are proved by using
Poposition 1. Let us illustrate the technique of proof by giving a proof to (5). Suppose that  A-(B
A-(B C).
C). A
A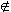 B
B C.
C. A
A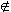 B
B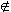 C. If
C. If 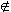 B,
B, A-B;
A-B;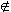 C,
C, A-C.
A-C.
 (A-B)
(A-B)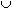 (A-C),
(A-C),and
 C)
C) (A-B)
(A-B)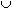 (A-C).
(A-C).Suppose that
 (A-B)
(A-B)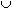 (A-C).
(A-C).Then either
 A-B
A-Bor
 A-C,
A-C,
so that  A
A A
A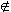 B
B C,
C, A-(B
A-(B C).
C).
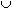 (A-C)
(A-C) A-(B
A-(B C).
C).By Poposition 1, we see that (5) holds.
Let A and B be sets. The Cartesian product of A and B is the set whose elements are pairs (a,b), where  A
A B.
B. B.
B. B
B
 B = {(1,1),(1,3),(2,1),(2,3)}.
B = {(1,1),(1,3),(2,1),(2,3)}.The most familiar example of a Cartesian product is the plane of analytic geometry, which consists of all ordered pairs (a,b) of real numbers a and b, and is thus the Cartesian product  R
R
Let us end this section with a few comments about logic. If P and Q are logical propositions, we will denote the implication "if P then Q" by 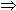 Q
Q P.
P.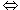 Q.
Q.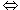 Q,
Q,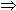 Q
Q Q.
Q.