 G,
G, G,
G, G,
G,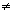
 .
. H,
H, H.
H. F[X],
F[X],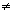 0.
0.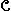 be a collection of subrings of R. Then
be a collection of subrings of R. Then 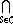 S is a subring of R.
S is a subring of R.
| Back | Table of Contents |
|
|
Subrings and Quotient RingsEarlier we introduced groups and then how to manufacture new groups from a given group by forming subgroups and quotient groups. In this section we will describe the analogous process of manufacture for rings. We will study the subrings and quotient rings of a given ring R. We will begin with subrings. Definition 1: Let R be a ring. A subset S of R is called a subring of R if S is a ring with respect to the operations of addition and multiplication in R. Example 1: Z is a subring of Q. Example 2: Q is a subring of R, the field of real numbers. Example 3: 2Z is a subring of Z. Example 4: Z[ Example 5: Let
T2(Q) =
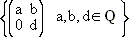 , ,
U2(Q) =
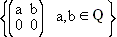 , ,
We assert that 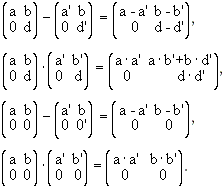
[Note that we need Proposition 2 from the section on subgroups to draw the conclusion that Example 6: Let R be any ring. Then R and {0} are subrings of R, called the trivial subrings. The observations of Example 5 lead to
Theorem 2: Let S be a nonempty subset of the ring R. Then S is a subring of R if and only if for Proof:
As an easy consequence of the above theorem, we can prove the following proposition.
Proposition 3: Let R be a ring and let 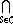 S Sis a subring of R. Proof: Let
S* =
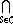 S, S,
and let
a - b, a · b
 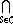 S = S*. S = S*.Therefore, by Theorem 2, S* is a subring of R. Suppose that R is a ring and that
[C] =
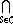 S. S.
By the above proposition, [C] is a subring of R. Moreover, [C] certainly contains C, since every Proposition 4: Let C be a subset of the ring R. Then [C] is the smallest subring or R which contains C. The subring [C] is called the subring generated by the set C. Let us give some examples. If
[C] = {a0 + a2X2 + a4X4 + ... + a2tX2t | a2t
 F}. F}.After our brief study of subrings, let us now look at quotient rings. Let R be a ring, S a subring of R. In particular, S is a subgroup of the additive group of R. Since the additive group of R is commutative by the definition of a ring, S is a normal subgroup of the additive group of R. Thus, by our previous group-theoretical results, the set of cosets R/S becomes a group with respect to the law of addition:
(r + S) + (r' + S) = (r + r') + S,
where (1)
(r + S)·(r' + S) = r · r' + S.
The principal difficulty with this definition is that the product of (2)
(r + s + S) · (r' + s' + S) = (r + S) · (r' + S),
for all
r · r' + s · r' + r · s' + s · s' + S = r · r' + S
Since
s · r' + r · s'
 S, S,
where (3) must hold for all
r · s'
 S, s · r' S, s · r'  S S
for Let ~ denote the equivalence relation on R defined by:
Definition 5: Let R be a ring. An ideal of R is a subring I of R such that if Note that if R is commutative, then the two conditions Example 7: Let R be any ring. then {0} and R are subrings of R and it is clear that these subrings are ideals. These ideals are called the trivial ideals. Example 8: Let R = Z. We have seen that nZ = {n · r | r
(n · r) · s = n · (r · s)
 nZ. nZ.Therefore, nZ is an ideal of Z. In general, we see that every subgroup of Z is a subring. Example 9: Let F be a field. X an indeterminate over F,
fF[X] = {f · g | g
 F[X]}. F[X]}.Then fF[X] is an ideal of F[X]. Example 10: Let F be a field, F[X,Y] the ring of polynomials in two indeterminates X and Y over F. Set
(X,Y) = {X · f + Y · g | f,g
 F[X,Y]}. F[X,Y]}.Then (X,Y) consists of all polynomials with zero constant term and is an ideal of F[X,Y]. Example 11: Let R be any commutative ring,
aR = {a · r | r
 R}. R}.
Then aR is an ideal of R. If Before delving any further into the theory of ideals, lets complete our construction of quotient rings. Let R be a ring and let us recall how we were led to the notion of an ideal. We started with a subring S of R and asked whether the multiplication (1) actually makes sense. We found that this is the case if and only if S is an ideal of R.
Proposition 6: Let R be a ring, I an ideal of R, R/I is the set of cosets of the form
(a + I) + (b + I) = (a + b) + I (a,b
 R), R),and we define multiplication of cosets by (6)
(a + I) · (b + I) = ab + I.
Then with respect to these operations, R/I becomes a ring, called the quotient ring of R with respect to I. Proof: From our discussion above, R/I is an abelian group with respect to the law of addition (5). Moreover, we showed that the law of multiplication (6) makes sense, since I is an ideal. Multiplication is associative: For if
(a + I) · [(b + I) · (c + I)] = (a + I) · (b · c + I)
= a · (b · c) + I
= (a · b) · c + I
= (a · b + I) · (c + I)
= [(a + I) · (b + I)] · (c + I).
Similarly, the distributive laws in R imply the corresponding laws in R/I. Thus R/I is a ring. Proposition 7: Let R be a ring, I an ideal of R. Then (1) If R is commutative, then R/I is commutative. (2) If R is a ring with identity 1, then R/I is a ring with identity Let us return to the examples of ideals which we gave above and lets describe the corresponding quotient rings. Example 12: Example 13: Let R be any ring, I a trivial ideal of R - that is,
a + {0} (a
 R). R).
Two such cosets
a
 a + {0}. a + {0}.
Addition and multiplication in R/{0} corresponds to addition and multiplication in R under this correspondence. Thus, R/{0} is "essentially" R. (Strictly speaking, R/{0} is isomorphic to R.) Assume now that Example 14: Let F be a field,
g + I = g + f · h + I, h
 F[X]. F[X].From all these different representations for the coset
g + I = f · q + r + I = r + I.
Therefore, each coset
r = a0 + a1X + ... + an-1Xn-1 (ai
 F). F).
Moreover, if Let us consider a special case. Let
a0 + a1X + I, a0,a1
 Q. Q.The addition of cosets is given by
(a0+a1X+I) + (b0+b1X+I) = (a0+b0) + (a1+b1)X + I
The multiplication of cosets is defined by
(a0 + a1X + I) · (b0 + b1X + I)
= a0b0 + (a1b0)X + a1b1X2 + I
= (a0b0 + 2a1b1) + (a1b0 + a0b1)X + a1b1(X2 - 2) + I
= (a0b0 + 2a1b1) + (a1b0 + a0b1)X + I
Note that the above addition and multiplication are very similar to the corresponding operations on the ring Let us close this section by determining all the subrings of a quotient ring R/I. Proposition 8: Let R be a ring, I an ideal of R. If S is a subring of R containing I, then S/I is a subring of R/I. Conversely, every subring of R/I is of the form S/I, where S is a subring of R which contains I. Proof:
(s + I) - (t + I) = (s - t) + I
 S/I, S/I,
(s + I) · (t + I) = s · t + I
 S/I. S/I.Thus, by Proposition 3, S/I is a subring of R/I. Conversely, let |
| Back | Table of Contents |