 B
B B
B B
B B
B A
A S
S R
R S
S T
T T
T I,
I, R,
R, I
I I.
I.
| Back | Table of Contents |
|
|
Isomorphisms and HomomorphismsIn this section we will imitate our approach in the theory of groups, whereby we introduced isomorphisms and homomorphisms between groups.
Definition 1: Let R and S be rings. A ring homomorphism from R to S is a function (a) (b) Note that in condition (a) the sum on the left refers to addition in R, while the sum on the left refers to addition in S. Similar comments apply to the multiplication in (b). Condition (a) implies that a ring homomorphism is a homomorphism from the additive group of R to the additive group of S. Therefore, we may apply our results on group homomorphisms to get that (1)
f(-a) = -f(a) (a
(2)
 R), R),
f(0) = 0.
[Note that there is a slight ambiguity in (2). The zero on the left refers to the zero element of R, while the zero on the right refers to the zero element of S.]
Definition 2: Let R and S be rings. A ring homomorphism Example 1: Let R be any commutative ring, X indeterminate over R,
f(a) = a0 + a1a + ... + anan.
Let  a(f ) = f(a) (f a(f ) = f(a) (f  R[X]). R[X]).
Then
g = b0 + b1X + ... + bnXn + ...  R[X] R[X]
then  a(f + g) = a(f + g) =  a((a0+b0)+(a1+b1)X+...+(an+bn)Xn+...) a((a0+b0)+(a1+b1)X+...+(an+bn)Xn+...)
= (a0+b0)+(a1+b1)a+...+(an+bn)an+...
= (a0 + a1a + ... + anan + ...)
+(b0 + b1a + ... + bnan + ...)
=
 a(f) + a(f) +  a(g). a(g).Similarly, since
f · g = c0 + c1X + ... + cnXn + ...,
where
ci = a0bi + a1bi-1 + ... +aib0,
we see that
= (a0 + a1a + ...)·(b0 + b1a + ...) (R is commutative)
=
Therefore, Example 2: Let
f(x + y) = x + y = x + y = f(x) + f(y),
f(x · y) = x · y = x · y = f(x) · f(y),
Therefore Example 3: Let
f(a +
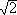 ) = a - b ) = a - b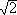 Then f is a ring homomorphism. It is trivial to see that f is injective, so that f is an isomorphism. Example 4: Let
f(a0 + a1X + I) = a0 + a1
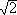 Then the mapping f was discussed in the previous section. It is a consequence of that discussion that f is a surjective isomorphism. Therefore, Example 5: Let R be any ring and let S be any ring. The mapping
f :R
 S, S,
f(x) = 0 (x
 R) R)is called the zero homomorphism. Example 6 Let R be any ring, I an ideal of R. Let us define the mapping  I:R I:R R/I, R/I, I(x) = x + I (x I(x) = x + I (x  R). R).Then by the definitions of addition and multiplication in R/I.  I(x + y) = (x + y) + I I(x + y) = (x + y) + I
= (x + I) + (y + I)
=
 I(x) + I(x) +  I(y), I(y), I(x · y) = x · y + I I(x · y) = x · y + I
= (x + I) · (y + I)
=
 I(x) · I(x) ·  I(y). I(y).
Therefore,
Lemma 3: Let R and S be rings and let Proof: First note that it makes sense to speak of
f -1(x + y) = f -1(x) + f -1(y),
(3)
f -1(x · y) = f -1(x) · f -1(y).
Since f is a homomorphism,
f(f -1(x) + f -1(y)) = f(f -1(x)) + f(f -1(y))
(4)
= x + y,
f(f -1(x) · f -1(y)) = f(f -1(x)) · f(f -1(y))
(5)
= x · y,
By applying
Lemma 4: Let Proof: Let Proposition 5: Ring isomorphism is an equivalence relation. That is, the following properties hold. Let R, S, and T be rings. (1) R (2) If (3) If Proof: (1) If (2) If (3) If Just as was the case in the theory of groups, it is easy to see that isomorphic rings have identical properties differing only in the naming of the elements. The surjective ring isomorphisms preserve completely the structure of a ring. Although homomorphisms do not preserve all of the properties of a ring, they nevertheless preserve a number of very significant properties. The next proposition gives us some examples of properties preserved by homomorphisms.
Proposition 6: Let R and S be rings, (1) If U is a subring of R, then Moreover, if f is surjective, then the following are true (2) If R is commutative, then S is commutative. (3) If R has an identity 1, then S has an identity Proof: (1) Let
x - y = f(r) = f(t) = f(r - t),
xy = f(r)f(t) = f(rt).
Therefore, (2) Let (3) Let Note that without the surjectivity of f, assertions (2) and (3) are false. In analogy with the situation in group theory, let us define the kernel of the ring homomorphism
{r
 R | f(r) = 0}. R | f(r) = 0}.
Let us denote the kernel of f by 1'. If 2'. If 3'. If 4'. If 5'. If R is any ring and 6'. If R is any ring, I an ideal in R, In group theory, the kernel of a homomorphism is always a normal subgroup, whereas the kernel of an isomorphism consists of just the identity element. These facts generalize to ring homomorphisms:
Proposition 7: Let R and S be rings, (1) (2) f is an isomorphism if and only if Proof: Since f is a homomorphism from the additive group of R to the additive group of S, our results on group homomorphisms imply (a) that
= 0.
Therefore, Let us now take up the ring analogue of the first isomorphism theorem of group theory. Let R and S be rings and let 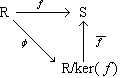
is commutative - that is,
Theorem 8 (First Isomorphism Theorem of Ring Theory) Let R and S be rings, and let 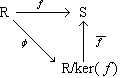
is commutative. In particular, The interpretation of Theorem 8 is analogous to the interpretation of the corresponding theorem for groups. On one hand, the theorem asserts that up to isomorphism, all homomorphisms of rings can be obtained as canonical homomorphisms. On the other hand, the first isomorphism theorem gives us a way of guaranteeing the existence of isomorphism without having to actually write them down. |
| Back | Table of Contents |