The Complex Numbers
The complex numbers C are introduced in high school as the set of all quantities of the form a + bi, where a and b are real numbers and i = 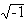 . This last condition means simply that i2 = -1. We say that two complex numbers a + bi and c + di are equal if a = c and b = d. Further, we define addition and multiplication of complex numbers by . This last condition means simply that i2 = -1. We say that two complex numbers a + bi and c + di are equal if a = c and b = d. Further, we define addition and multiplication of complex numbers by
(1)
(a + bi) + (c + di) = (a + c) + (b + d)i,
(2)
(a + bi) · (c + di) = (ac - bd) + (ad + bc)i.
With respect to these operations, C becomes a field. The additive identity is 0 + 0i and the multiplicative identity is 1 + 0i. The additive inverse of a + bi is (-a) + (-b)i, while if a + bi is nonzero, then either a 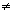 0 or b 0 or b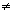 0 and the multiplicative inverse of a + bi is 0 and the multiplicative inverse of a + bi is
We will leave the verification of these facts, as well as the associativity, commutativity, and distributivity laws for the reader to check. Note that we may regard the real numbers R to be a subfield of C by defining a  R with the complex number a + 0i. More precisely, the mapping R with the complex number a + 0i. More precisely, the mapping
a  a + 0i
is an isomorphism. In what follows, we will always regard R as a subfield of C.
All of the above is probably more or less familiar from high school algebra. However, there is a basic defect with the above definition of C. In our above explanation, we have introduced i = 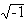 . And it is not at all clear what i is or where it comes from. This gives complex numbers a somewhat mysterious quality and accounts for the terminology which calls i an "imaginary number." The way out of this logical morass was discovered by Gauss in his dissertation. Instead of considering quantities of the form a + bi, let us consider ordered pairs (a,b). We say that two ordered pairs (a,b) and (c,d) are equal if a = c and b = d. We define addition and multiplication of the ordered pairs via . And it is not at all clear what i is or where it comes from. This gives complex numbers a somewhat mysterious quality and accounts for the terminology which calls i an "imaginary number." The way out of this logical morass was discovered by Gauss in his dissertation. Instead of considering quantities of the form a + bi, let us consider ordered pairs (a,b). We say that two ordered pairs (a,b) and (c,d) are equal if a = c and b = d. We define addition and multiplication of the ordered pairs via
(1')
(a,b) + (c,d) = (a + c, b + d),
(2')
(a,b) · (c,d) = (ac - bd, ad + bc).
We define C to be the set of all these ordered pairs. With respect to the addition (1') and multiplication (2'), C becomes a field. Moreover, R may be identified with the subfield {(a,0) | a  R} of C. Thus we have explicitly constructed a field C containing R. Consider the element (0,1) of C. From the definition of multiplication in C, R} of C. Thus we have explicitly constructed a field C containing R. Consider the element (0,1) of C. From the definition of multiplication in C,
(0,1) · (0,1) = (-1,0).
That is, (0,1)2 equals -1. Thus, our field C contains a square root of -1. Let us set i = (0,1). Then every complex number can be uniquely written in the form a + b · i, where a,b  R. The field C which we have constructed is precisely what we are accustomed to think of as the field of complex numbers. R. The field C which we have constructed is precisely what we are accustomed to think of as the field of complex numbers.
Let us proceed to study the properties of the complex numbers in somewhat more detail. If  = a + ib = a + ib  C, we define the complex conjugate C, we define the complex conjugate 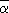 of of  by by
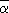 = a - ib.
The following are easily verified properties of complex conjugation: Let  , ,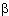  C. C.
I. 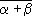 = = 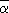 + + 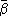 . .
II. 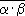 = = 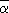 · · 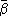 . .
III. 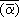 = =  . .
IV. 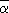 = =  if and only if if and only if  is real. is real.
V. The mapping   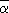 of C onto C is a surjective isomorphism which is the identity isomorphism on R.(This follows from I, II and IV.) of C onto C is a surjective isomorphism which is the identity isomorphism on R.(This follows from I, II and IV.)
VI.  · · 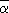 is a real number and is a real number and  · · 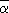 > 0. (In fact, if x = a + ib, then > 0. (In fact, if x = a + ib, then  · · 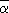 = a2 + b2 > 0.) = a2 + b2 > 0.)
We define the norm of the complex number a + ib to be a2 - b2.
Let us define the absolute value of  , denoted | , denoted | |, by |, by
By VI,  · · 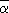 is a nonnegative real number, so | is a nonnegative real number, so | | makes sense and is a nonnegative real number. It is possible to give the absolute value of a complex number a geometric interpretation as follows: Let us associate to the complex number | makes sense and is a nonnegative real number. It is possible to give the absolute value of a complex number a geometric interpretation as follows: Let us associate to the complex number  = a + ib the point on the Cartesian plane with coordinates (a,b). Then this sets up a one-to-one correspondence between complex numbers and points of the Cartesian plane. Moreover, it is clear from Figure 1 that |a + ib| is just the distance of the point (a,b) from the origin. = a + ib the point on the Cartesian plane with coordinates (a,b). Then this sets up a one-to-one correspondence between complex numbers and points of the Cartesian plane. Moreover, it is clear from Figure 1 that |a + ib| is just the distance of the point (a,b) from the origin.
Figure 1: One-to-One Correspondence Between R2 and C. Let  = |a + ib| = = |a + ib| = 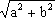 and let and let  be the angle which the line connecting the origin and (a,b) makes with the positive half of the x-axis. By the definitions of sin be the angle which the line connecting the origin and (a,b) makes with the positive half of the x-axis. By the definitions of sin and cos and cos , we know that , we know that
(3)
Therefore, we may represent the complex number a + ib in the form
(4)
This representation is called the polar form of a + ib and  is called the argument of a + ib. is called the argument of a + ib.
Let us illustrate geometrically the meaning of addition and multiplication of complex numbers. Let a + ib, c + id  C. Then C. Then
(a + ib) + (c + id) = (a + c) + i(b + d)
corresponds geometrically to the point (a + c, b + d). Thus, complex numbers add according to the usual "parallelogram law" of elementary physics (see Figure 2).
In order to describe multiplication, it is best to use the polar form. Let
a + ib =  1 1(cos  1 1 + i sin  1 1),
c + id =  2 2(cos  2 2 + i sin  2 2),
Then
(a + ib) · (c + id) =  1 1 2 2([cos  1 1cos  2 2 - sin  1 1sin  2 2]
+ i[cos  1 1sin  2 2 + cos  2 2sin  1 1])
=  1 1 2 2[cos(  1 1 +  2 2) + i sin(  1 1 +  2 2)].
Thus, (a + ib) · (c + id) corresponds to the point at distance  1 1 2 from the origin and has argument 2 from the origin and has argument  1 + 1 +  2. Note that we have used the addition formula for sin and cos, which should be familiar from trigonometry. From (5), an induction argument immediately shows that for n > 0, 2. Note that we have used the addition formula for sin and cos, which should be familiar from trigonometry. From (5), an induction argument immediately shows that for n > 0,
(6)
(a + ib) n =  n n[cos(n  ) + i sin(n  )].
This last formula is usually known as de Moivre's theorem. Let us use de Moivre's theorem to get some information about the nth roots of complex numbers.
Let  = =  (cos (cos + i sin + i sin ) be a complex number. Let us inquire as to whether ) be a complex number. Let us inquire as to whether  has any nth roots in C, where n is a positive integer. We say that has any nth roots in C, where n is a positive integer. We say that 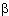 is an nth root of is an nth root of  if if 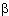 n = n =  . If . If  = 0, then = 0, then 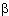 = 0 is an nth root, and is in fact the only nth root. Thus, let us assume that = 0 is an nth root, and is in fact the only nth root. Thus, let us assume that  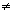 0. Then we have 0. Then we have  > 0. First observe that > 0. First observe that  has at most n nth roots in C, since any nth root of has at most n nth roots in C, since any nth root of  is a zero of the polynomial Xn - is a zero of the polynomial Xn -  , and this polynomial has at most n zeros. Next, consider the following n distinct complex numbers: , and this polynomial has at most n zeros. Next, consider the following n distinct complex numbers:
(7)
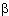 k k =  1/n 1/n[cos(  /n + 360/n · k) + i sin(  /n + 360/n · k)]
(k = 0,1,...,n - 1),
where  1/n is the positive nth root of 1/n is the positive nth root of  . By de Moivre's theorem, . By de Moivre's theorem,
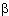 kn kn = (  1/n 1/n) n[cos(  + 360 · k) + i sin(  + 360 · k)]
=  .
Therefore, 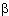 k is and nth root of k is and nth root of  and we have proved the following theorem. and we have proved the following theorem.
Theorem 1: Every nonzero complex number has n nth roots in C.
The formula (7) can be used to compute nth roots. For example let us look at the formula for the nth roots of 1. Since
1 = 1 · (cos 0 + i sin 0),
we see that the nth roots of 1 are given by
(8)
cos(360k/n) + i sin(360k/n) (k = 0,1,...,n - 1).
Let
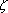 n n = cos(360/n) + i sin(360/n).
Then from (8), 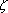 n is an nth root of 1, and in fact, corresponds to k = 1. Moreover, from de Moivre's theorem, we see that n is an nth root of 1, and in fact, corresponds to k = 1. Moreover, from de Moivre's theorem, we see that
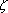 nk nk = cos(360k/n) + i sin(360k/n).
Therefore, from (8), we see that all the nth roots of unity are powers of 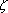 n. Thus, we have the following theorem. n. Thus, we have the following theorem.
Theorem 2: The nth roots of 1 in C form a cyclic group of order n. A generator of this group is 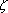 n. n.
We will denote the group of nth roots of unity by Xn. A generator of Xn is called a primitive nth root of unity. Since the order of 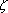 kn is n/(k,n), we see that the order of kn is n/(k,n), we see that the order of 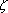 kn is n only if (k,n) = 1. Therefore, the primitive nth roots of unity are given by kn is n only if (k,n) = 1. Therefore, the primitive nth roots of unity are given by
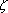 nk nk [0 < k < n - 1, (k,n) = 1].
There are exactly  (n) such roots of unity. (n) such roots of unity.
We found above that the n nth roots of a nonzero complex number  = =  (cos (cos + i sin + i sin ) are given by ) are given by 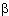 k (k = 0,...,n - 1). where k (k = 0,...,n - 1). where 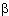 k is defined by (7). Note however, that by (5), we have k is defined by (7). Note however, that by (5), we have
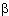 k k = (  1/n 1/n[cos(  /n) + i sin(  /n)])[cos(360k/n) + i sin(360k/n)]
= 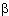 0 0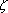 nk nk.
Thus we obtain the n nth roots of  by multiplying the fixed nth root by multiplying the fixed nth root 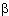 0 by all possible nth roots of unity. Therefore, we have 0 by all possible nth roots of unity. Therefore, we have
Theorem 3: Let  be a nonzero complex number. Let be a nonzero complex number. Let 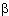 be an nth root of be an nth root of  . Then the nth roots of . Then the nth roots of  are all of the form are all of the form 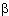 · · 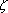 , where , where 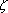 is an nth root of unity. Conversely, every such quantity is an nth root of is an nth root of unity. Conversely, every such quantity is an nth root of  . .
|
 B
B B
B A
A B
B B
B A
A S
S R,
R, :n
:n
 (n) = the number of integers a,
(n) = the number of integers a, 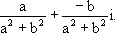
 a + 0i
a + 0i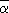 = a - ib.
= a - ib. | =
| =  =
= 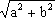 (
( = a + ib).
= a + ib).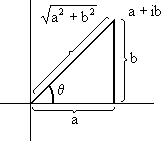
 cos
cos , b =
, b =  sin
sin .
. (cos
(cos + i sin
+ i sin ).
).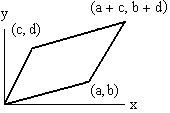
 1(cos
1(cos 1 + i sin
1 + i sin 1),
1), 2(cos
2(cos 2 + i sin
2 + i sin 2),
2), 1
1 2([cos
2([cos 1cos
1cos 2 - sin
2 - sin 1sin
1sin 2]
2] 1sin
1sin 2 + cos
2 + cos 2sin
2sin 1])
1]) 1
1 2[cos(
2[cos( 1 +
1 +  2) + i sin(
2) + i sin( 1 +
1 +  2)].
2)]. n[cos(n
n[cos(n ) + i sin(n
) + i sin(n )].
)].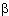 k =
k =  1/n[cos(
1/n[cos( /n + 360/n · k) + i sin(
/n + 360/n · k) + i sin( /n + 360/n · k)]
/n + 360/n · k)]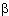 kn = (
kn = ( 1/n)n[cos(
1/n)n[cos( + 360 · k) + i sin(
+ 360 · k) + i sin( + 360 · k)]
+ 360 · k)] [cos
[cos + i sin
+ i sin ]
] .
.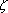 n = cos(360/n) + i sin(360/n).
n = cos(360/n) + i sin(360/n).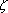 n is an nth root of 1, and in fact, corresponds to
n is an nth root of 1, and in fact, corresponds to 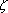 nk = cos(360k/n) + i sin(360k/n).
nk = cos(360k/n) + i sin(360k/n).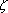 nk [0 < k < n - 1, (k,n) = 1].
nk [0 < k < n - 1, (k,n) = 1].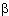 k = (
k = ( 1/n[cos(
1/n[cos( /n) + i sin(
/n) + i sin( /n)])[cos(360k/n) + i sin(360k/n)]
/n)])[cos(360k/n) + i sin(360k/n)]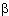 0
0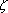 nk.
nk.