Historical Perspectives
The subject of algebra began thousands of years ago at the hands of the ancient Egyptians and Babylonians. Although their methods of solving algebraic problems have been lost to history, it seems clear that the accomplishments of their highly developed civilizations necessitated being facile with a wide spectrum of algebraic tools. For example, their vast architectural programs, astronomical calculations, and calendar computations must have required a practical knowledge of the solutions of linear and quadratic equations. The mathematics of the Babylonians and Egyptians is characterized by its empirical nature; They were more interested in the solutions to specific problems than the general techniques for solving them.
The great contribution of the Greeks to mathematics was, of course, the axiomatic method, which we must rank as one of the most original creations in the history of human thought. According to the Greek conception, geometry consisted of theorems, which are deduced, via an accepted method of logic, from a set of axioms. Of course, for the Greeks, there was a preferred set of axioms - the axioms of Euclidean geometry. They felt that this set of axioms had a certain metaphysical significance, reflecting the "true" geometrical state of the universe. And if the Greek's failure to recognize other axiom systems was a failure of Greek mathematics, then it was but a slight shortcoming when weighed against the successful development of the axiomatic method.
The geometric viewpoint of the Greeks led to certain shortcomings in their development of algebra. For example, the Greeks solved quadratic equations by "completing the square." However, negative roots were ignored since they did not have any geometrical significance. The introduction of negative numbers was due to the Hindus in the first centuries after Christ. Algebra prospered at the hands of the Hindus, who were much more oriented toward arithmetic than the Greek geometers. The algebra of the Hindus was brought westward by the Moslems, who embellished it considerably and gave the subject its current name. One of the most significant algebraic results which dates from the Moslem period is the quadratic formula, which is learned by every student of high school algebra. The formula asserts that the quadratic equation
has roots
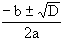
where D = b2 - 4ac is the discriminant of the equation.
Mathematicians searched for several hundred years to find a "cubic formula" which could be used to solve cubic equations in much the same way that the quadratic formula is used to solve quadratic equations. Such a formula was discovered by the Italian mathematician (The early Italian algebraists were known as the Cossists from the Italian word cosa (thing), since they solved equations for an unkown cosa.) Tartaglia (1506?-1557). However a contemporary and fellow-countryman of Tartaglia, Cardan (1501-1576), first published Tartaglia's solution of the cubic equation (without Tartaglia's permission), and history cruelly gives credit for the solution of the general cubic to Cardan. The general cubic equation is of the form
(1)One of Tartaglia's discoveries was the observation that if one performs the change of variable
The cubic can be put in the form:
(2)Therefore, it suffices to consider equations of the later form. Let
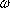 = (-1 +
= (-1 + 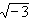 )/2.
)/2.Then 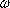 is a cube root of 1; that is
is a cube root of 1; that is 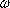 3 = 1. In fact, the three cube roots of 1 are given by
3 = 1. In fact, the three cube roots of 1 are given by
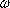 ,
, 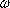 2.
2.Let X1, X2, and X3 be roots of the cubic. Then Tartaglia, by using some very clever arguments, found that
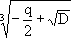 +
+ 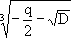
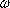
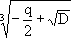 +
+ 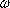 2
2 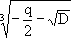
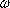 2
2  +
+ 
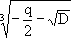
where
is the discriminant of the cubic. On examining Tartaglia's formulas, it is hard not to admire their beauty and to envy the cleverness of the man who
discovered them. The above formulas for X1, X2, and X3, appear very strange, especially because of the complex number 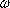 . Nothing
analogous occurs in the case of the quadratic equations. Nevertheless, it is not possible to find a solution of the general cubic which does not involve complex numbers. To solve a cubic, see the example.
. Nothing
analogous occurs in the case of the quadratic equations. Nevertheless, it is not possible to find a solution of the general cubic which does not involve complex numbers. To solve a cubic, see the example.
In 1545, Cardan's pupil, Ferrari, obtained the solution of the general fourth-degree (or biquadratic) equation. Ferrari's formulas are along the same lines as Tartaglia's, only much more complicated.
After Tartaglia's and Ferrari's successes in treating equations of the third and fourth degree, there was a feeling of optimism in the mathematical community that within a short time, a "general solution" of equations of the fifth and higher degree would be discovered. We should ponder for a moment what we mean by a "general solution" of an equation of degree n. Based on our experience with equations of degree 2 and 3, let us understand by a "general solution" of the nth-degree equation a set of formulas which allow the calculation of the n roots of the equation of degree n as functions of the coefficients. Moreover, the formulas should involve only arithmetic operations (addition, subtraction, multiplication, and division) and the extraction of roots. Much effort was expended in search of such a general solution. However, two centuries elapsed without any real progress.
The first real breakthrough was due to Joseph-Louis Lagrange, who, in the late eighteenth century, gave a uniform technique for solving equations of degree at most 4, thereby incorporating a single method all that was known about general solutions to equations. His idea was to reduce the solution of a given equation to the solution of certain auxiliary equations called resolvents. In case the degree of the given equation is at most 4, the resolvents are of lower degree than the given equation, so that starting with quadratic equations, the method of Lagrange can be used to give successively, the solution to quadratic, cubic, and biquadratic equations. However, Lagrange's method breaks down in the case of fifth-degree(quintic) equations, because the resolvent which his method associated with a quintic is of sixth degree.
The failure of Lagrange's method to solve the quintic suggested the startling possibility that no general solution of the quintic exists. This is indeed the case and was first proved by Neils Heinrik Abel in 1828. What Abel's theorem states is that it is impossible to find a general formula for the roots of a quintic equation if the formula is only allowed to use arithmetic operations and extraction of roots. However, what is even more surprising is the fact that there exist particular quintic equations, with ordinary integers as coefficients, whose roots cannot be expressed in terms of arithmetic operations and extraction of roots. It is important to recognize that Abel's theorem required a very novel proof. It is fairly easy to determine whether or not a given formula provides a solution of a given equation. But to prove that no formula can be written down is quite a different matter.
A necessary and sufficient condition that a given equation be solvable in radicals(i.e., in terms of arithmetic operations and extraction of roots) was given by Evariste Galois in 1830. A child prodigy, who was killed in a duel before he was 21, Galois laid the foundations for the modern theory of equations. Galois' brilliant ideas were incredibly sophisticated for his day and were not acknowledged by is contemporaries. It was not until several decades after the death of Galois that his great contributions were first appreciated. At this point we cannot state Galois' results with any kind of precision; nevertheless, let us try to get the flavor of Galois's ideas by considering some examples.
Let us consider a polynomial
having roots
where we have labeled the roots in some fixed (but otherwise arbitrary) order. A permutation of the roots is a rearrangement of X1,...,Xn of the form
where the set i1,...,in consists precisely of the integers 1,2,...,n each appearing once. It is often convenient to think of a permutations as replacing X1 by Xi1, X2 by Xi2, and so forth. For this reason, it is often convenient to denote a permutation by the symbol

where the notation indicates that Xj is to be replaced by Xij
The basic idea of Galois was to associate to the polynomial
a certain collection of permutations belonging to Sn and depending on the coefficients. The set of permutations forms a mathematical structure known as a group and is called the Galois group of the polynomial. At this point we do not want to digress to precisely define the notion of a group, nor do we wish to describe how we arrive at the Galois group. However, to get the flavor of this concept, consider a few examples.
Example 1: X2 - 2. Here the Galois group is S2 and consists of the permutations
 and
and 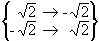 .
.Example 2: (X2 - 2)(X2 + 1). Here the Galois group is a subgroup of S4 consisting of the permutations
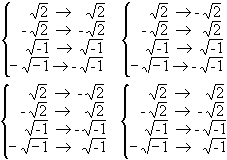
The algebraic properties of a polynomial are mirrored by the Galois group. For example, solvability by radicals of the equation determined by a polynomial is translated into a very simple property of the Galois group. And when a given equation is solvable in radicals, the properties of Galois group enable one to write down the solution in radicals. In fact, if a given equation is solvable in radicals, the solution can always be obtained from the Galois group using a fixed procedure. And when this fixed procedure cannot be carried out, the equation cannot be solved in radicals. In this way we can establish both Abel's theorem on the insolubility of the quintic and the formulas for the quadratic, cubic, and biquadratic equations. If all this sounds somewhat obscure, we hope to clarify matters later.
The problem of solving polynomial equations led mathematicians to study groups and is thus one of the historical cornerstones on which contemporary algebra is based. The introduction of groups into mathematics and the great triumphs in the theory of equations had a very profound influence on many fields of mathematics which were undergoing development in the early nineteenth century. One of these fields was geometry. Although the influences of algebra on geometry were many, let us be content to cite three examples.
The Greek geometers were interested in the problem of constructing geometrical figures using a straightedge and compass, and by the time of Euclid, many such constructions were known. For example, the Greeks knew how to bisect a line segment, bisect an angle, construct a line perpendicular to a given line, and even construct a regular pentagon. However, there were three seemingly elementary constructions, which the Greeks were unable to solve. The first was to trisect an angle; that is to construct an angle equal to one third of a given angle. The second was to construct a cube whose volume was twice that of a given cube. The third was to construct a square whose area was the same as that of a given circle. It was finally shown in the nineteenth century that these three classical problems have no solution. That is, the required constructions cannot be carried out in general, at least if the only tools allowed are a straightedge and compass. It is rather amazing that the proof of the impossibility of these three classical problems used the ideas of algebra and not those of geometry. Perhaps even more surprising was the fact that the relevant algebraic ideas came from the theory of equations and the work of Galois. There will be a detailed description of these classical geometry problems later.
The nineteenth century was a time of great ferment in the field of geometry. The chief feature of this period was the emergence of many new systems of geometry, which satisfied all the axioms of Euclid's geometry except for the axiom which asserts that if we a given a line and a point off of the line, there is one and only one line passing through the given point and parallel to the given line. Once the first such geometry was created, many more followed, and in the middle of the nineteenth century there was a fundamental confusion about the axioms and goals of geometry. In the later part of the nineteenth century, Felix Klein proposed the idea of unifying all these different geometries around the notion of a group, a notion which had been created, as we have seen, for an entirely different purpose. Klein's conception of geometry was called the Erlangen program.
A third point of contact between algebra and geometry in the nineteenth century was the theory of algebraic curves, which received great impetus through the brilliant ideas of German mathematician Bernhard Riemann. Roughly speaking, an algebraic curve is the set of all ordered pairs of complex numbers (x,y) which satisfy an equation of the form
where a1(x), a2(x), ..., an(x) are polynomials with complex coefficients. Examples of algebraic curves are given by the solutions (in complex numbers) of the equations
XY = 1,
X3 = Y2 + Y3 + XY.
You are probably accustomed to thinking of an algebraic curve as a solution in real numbers (x,y) of an equation. The reason for considering complex solutions is to avoid examples of curves with
no points on them. For example the equation
Nor was geometry the only field which experienced a fruitful interchange with the field of algebra in the nineteenth century. Another field was the theory of numbers. Roughly speaking, the theory of numbers is a branch of mathematics which studies the properties of the integers:
It is one of the most difficult fields of mathematics, which for centuries has been the source of countless ideas for other branches of mathematics. Although it is impossible to describe completely all the algebraic ideas which arose in the consideration of problems in the theory of numbers, lets look at one well known example.
In the early part of the seventeenth century, Pierre Fermat, an amateur mathematician, claimed to have proved that if n is an integer greater than or equal to 3, it is impossible to find nonzero integers, x, y, and z such that
Fermat never wrote down his proof, and it seems unlikely that he actually had a proof. Indeed, three and one-half centuries later, until 1994, no one could
prove or disprove Fermat's assertion. A particularly good try at proving Fermat's statement was made by German mathematician
Ernst Kummer in 1835. It was subsequently pointed out to Kummer by Lejeunne Dirichlet that Kummer's alleged proof
was actually wrong, but for a rather intriguing reason. Kummer then made a very detailed study of his proof in order to better understand why it was wrong. As a result of
this study, Kummer was able to make his proof correct for certain values on n by using a new algebraic idea, the concept of an ideal. Today, the notion of an
ideal is on of the basic ideas in the theory of rings. We'll study more about rings later and retrace Kummer's reasoning for the case of