|
The Symmetric Groups
In the last section we proved that every finite group is isomorphic to a subgroup of Sn for some n. Therefore, the symmetric groups play a much more fundamental role in group theory than it would appear at the outset. In this section we will begin an in depth study of these groups.
Before we begin discussing the properties of Sn, let us introduce some new notation. Suppose that i1,...,ir are distinct integers, 1 < ij < n. Let
(i1i2...ir)
denote the permutation of Sn which maps i1 onto i2, i2 onto i3,..., and ir onto i1, and which leaves fixed the integers not expressly listed. Such a permutation is called an r-cycle. For example, the permutation (123) of S3 would be written in our old notation as
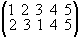 .
Any 1-cycle is the identity permutation. Moreover,
(1)
(i1,i2...ir)-1 = (irir-1...i1).
We will say that two cycles are disjoint if they have no elements in common. For example, (123) and (456) are disjoint. It is clear that disjoint cycles commute with one another. Note, however, that the product of two cycles is not necessarily a cycle, but only a permutation. We say that an r-cycle is nontrivial if r  1. 1.
Lemma 1: Let   Sn, Sn,   1. Then 1. Then  can be written as a product on nontrivial disjoint cycles, This representation is unique up to the rearrangement of the cycles. can be written as a product on nontrivial disjoint cycles, This representation is unique up to the rearrangement of the cycles.
We will postpone the proof of Lemma 1 for a moment. The following should suggest a proof to the reader. Let   S8 be given by S8 be given by
 = 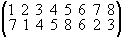
Then,  maps 1 into 7, 7 into 2, and 2 back to 1. Thus, (172) is a component of maps 1 into 7, 7 into 2, and 2 back to 1. Thus, (172) is a component of  . Moreover, . Moreover,  maps 3 into 4, 4 into 5, 5 into 8, and 8 back to 3. Thus, a second component cycle of maps 3 into 4, 4 into 5, 5 into 8, and 8 back to 3. Thus, a second component cycle of  is (3458). Finally, 6 is mapped into 6, so that is (3458). Finally, 6 is mapped into 6, so that  = (172)(3458)(6). Moreover, since a 1-cycle is the identity, we have = (172)(3458)(6). Moreover, since a 1-cycle is the identity, we have
 = (172)(3458),
as an expression of  as a product of nontrivial, disjoint cycles. as a product of nontrivial, disjoint cycles.
Proof of Lemma 1: We say that an integer i is fixed by  if if  (i) = i. Let us show how to express (i) = i. Let us show how to express  as a product of nontrivial, disjoint cycles by using induction on the number of integers not left fixed by as a product of nontrivial, disjoint cycles by using induction on the number of integers not left fixed by  . Thus . Thus  (i1) = i2, i2 (i1) = i2, i2  i1. If i1. If  (i2) (i2)  i1,i2, define i3 by i3 = i1,i2, define i3 by i3 =  (i2). If (i2). If  (i3) (i3)  i1,i2,i3, define i4 by i4 = i1,i2,i3, define i4 by i4 =  (i3),
and so on. Thus we define a sequence of integers i1,i2,...is, all distinct, and such that (i3),
and so on. Thus we define a sequence of integers i1,i2,...is, all distinct, and such that  (ik) = ik+1. Eventually, this process must stop, and (ik) = ik+1. Eventually, this process must stop, and  (is) will be one of i1,...is. But then (is) will be one of i1,...is. But then  (is) = i1. For if (is) = i1. For if  (is) = ik (1 < k < s), then (is) = ik (1 < k < s), then  maps both is and ik-1 onto ik, which contradicts the fact that maps both is and ik-1 onto ik, which contradicts the fact that  is a bijection. Set is a bijection. Set  = (i1i2,...is). Then = (i1i2,...is). Then   -1 fixes precisely i1,...,is and all the integers fixed by -1 fixes precisely i1,...,is and all the integers fixed by  . Therefore, . Therefore,   -1 has fewer integers not left fixed than -1 has fewer integers not left fixed than  . Thus by induction . Thus by induction   -1 = c1...ct, where c1,...,ct are nontrivial, disjoint cycles. Moreover integers appearing in c1,...,ct are just those not fixed by -1 = c1...ct, where c1,...,ct are nontrivial, disjoint cycles. Moreover integers appearing in c1,...,ct are just those not fixed by   -1. Thus, c1,...,ct are disjoint from -1. Thus, c1,...,ct are disjoint from  and and  = =  c1,...,ct is an expression of c1,...,ct is an expression of  as a product of nontrivial, disjoint cycles. The uniqueness is left to the reader. as a product of nontrivial, disjoint cycles. The uniqueness is left to the reader.
Definition 2: A transposition is a 2-cycle (ij), i  j. j.
A simple inductive argument suffices to show that Sn contains n(n-1)/2 transpositions.
Proposition 3: Sn is generated by the set of transpositions.
Proof: Let   Sn, Sn,   1. We will show that 1. We will show that  can be written as a product of transpositions. Let can be written as a product of transpositions. Let
(2)
 = (i 1i 2...i r)(j 1...j s)(k 1...k t)...
be the expression of  as a product of disjoint, nontrivial cycles. Then as a product of disjoint, nontrivial cycles. Then
(3)
 = (i 1i r)(i 1i r-1)...(i 1i 2)(j 1j s)...(j 1j 2)(k 1k t)...(k 1k 2)...
We see from the proof of proposition 3 that   Sn, Sn,  the identity, then the identity, then  can be written as a product of N( can be written as a product of N( ) transpositions, where ) transpositions, where
N(  ) = (r-1) + (s-1) + (t-1) + ...,
and  is given by (2). Let us set is given by (2). Let us set
N(1) = 0.
Note that although   1 can always be expressed as a product of N( 1 can always be expressed as a product of N( ) transpositions, it will usually be possible to write ) transpositions, it will usually be possible to write  as a product of some other number of transpositions. The next result will be used to prove that in any two such representations of as a product of some other number of transpositions. The next result will be used to prove that in any two such representations of  , the number of transpositions is always even or odd. , the number of transpositions is always even or odd.
Let  , ,   Sn. Then N( Sn. Then N(  ) )  N( N( ) + N( ) + N( ) (mod 2). ) (mod 2).
Theorem 4: Let  , ,   Sn. Then N( Sn. Then N(  ) )  N( N( ) + N( ) + N( ) (mod 2). ) (mod 2).
Proof: First we assert that it suffices to prove the theorem in the case  = a transposition. For assume that we know this special case, and let = a transposition. For assume that we know this special case, and let  and and  be arbitrary permutations; let be arbitrary permutations; let
be expressions of  and and  , respectively, as products of transpositions. Then, by induction and the assumed special case of the theorem, it is easy to verify that , respectively, as products of transpositions. Then, by induction and the assumed special case of the theorem, it is easy to verify that
N(   )  (N(  1 1)+N(  2 2)+...+N(  a a)) +
(N(  1 1)+...+N(  b b)) (mod 2)
Thus, let us assume that  = (ij), and let us assume that = (ij), and let us assume that  is given by (2) above. There are four cases to consider: is given by (2) above. There are four cases to consider:
Case 1: Neither i nor j appears in the cycle decomposition (2). In this case, N(  ) = (2 - 1) + (r - 1) + (s - 1) + (t - 1) +...= 1 + N( ) = (2 - 1) + (r - 1) + (s - 1) + (t - 1) +...= 1 + N( ) = N( ) = N( ) + N( ) + N( ). ).
Case 2: Exactly one of i and j appears in the cycle decomposition (2). Without loss of generality, let us assume that i = i1. Then
(ij)  = (jii 2...i r)(j 1...j s)(k 1...k t)... Therefore,
N(   ) = 1 + N(  ) = N(  ) + N(  ). Case 3: Both i and j appear in the cycle decomposition (2), but they appear in different cycles. Without loss of generality, assume that i = i1 and j = j1. Then
(ij)  = (jj 2...j sii 2...i r)(k 1...k t)... so that
N(   ) = (r + s -1) + (t - 1)+... = N(  ) + N(  ).
Case 4: Both i and j appear in the same cycle. Without loss of generality, let i = i1, j = ik. Then
(ij)  = (ii 2...i k-1)(ji k+1...i r)(j 1...j s)(k 1...k t)... so that
N(   ) = (k - 2) + (r - k) + (s - 1) + (t - 1) + ...
= N(  ) + N(  ) - 2
Definition 5: Let   Sn. Then Sn. Then  is even (respectively, odd) if N( is even (respectively, odd) if N( ) is even (respectively, odd). ) is even (respectively, odd).
Thus a permutation  is even if, when is even if, when  is written in the standard way as a product of transpositions, the number of transpositions is even. However, if is written in the standard way as a product of transpositions, the number of transpositions is even. However, if  is even and if is even and if  = =  1... 1... a is any expression of a is any expression of  as a product of transpositions, Theorem 4 and a simple induction imply that as a product of transpositions, Theorem 4 and a simple induction imply that
N(  )  N(  1 1 + ... + N(  a a) (mod 2)
 a (mod 2),
and thus a is even. Thus, a permutation is even if and only if it can be expressed (in any manner) as a product of an even number of transpositions.
By Theorem 4 and the fact that N( -1) = N( -1) = N( ), we see that the set of even permutations of Sn form a subgroup. This subgroup is call the alternating group on n elements and is denoted An. ), we see that the set of even permutations of Sn form a subgroup. This subgroup is call the alternating group on n elements and is denoted An.
Theorem 6:
(1) An is a normal subgroup of Sn.
(2) If n > 2, the index of An in Sn is 2.
Proof: Let us consider the mapping
 : S n  Z2 Z2
By Theorem 4, this mapping is a homomorphism. Its kernel is clearly An. Thus, part (1) is proved by Proposition 3 of the section on homomorphism. If n > 2, Sn contains the 2-cycle (12) and N((12)) = 1. Therefore, if n > 2,  is surjective. By the first isomorphism theorem, Sn/An is surjective. By the first isomorphism theorem, Sn/An Z2. Therefore, the index of An in Sn is 2. Z2. Therefore, the index of An in Sn is 2.
Earlier we proved that Sn is generated by the set of all transpositions. Let us now prove an analogous statement for An.
Proposition 7: An is generated by the set of all 3-cycles (ijk).
Proof: Let S denote the set of all 3-cycles, G = [S]. If n < 2, S =  , so that G = {1}. (The smallest subgroup of Sn containing S is just {1}.) But if n < 2, then An = {1}. Thus we may assume that n > 3. Since a 3-cycle is even, it is clear that G , so that G = {1}. (The smallest subgroup of Sn containing S is just {1}.) But if n < 2, then An = {1}. Thus we may assume that n > 3. Since a 3-cycle is even, it is clear that G 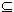 An. Let us prove the reverse inclusion. Since a permutation is even if and only if it can be written as a product of an even number of transpositions, we see that An is generated by all products of the form (i1i2)(i3i4) (i1 An. Let us prove the reverse inclusion. Since a permutation is even if and only if it can be written as a product of an even number of transpositions, we see that An is generated by all products of the form (i1i2)(i3i4) (i1  i2, i3 i2, i3  i4). Therefore it suffices to show that every such product is contained in the group G. There are three cases to examine: i4). Therefore it suffices to show that every such product is contained in the group G. There are three cases to examine:
Case 1: Only two of the integers ij(j=1,2,3,4) are distinct. Without loss of generality, we may assume that i1 = i3, i2 = i4. Then
(i 1i 2)(i 3i 4) = 1  G. Case 2: Three of the integers i1, i2, i3, and i4 are distinct. Without loss of generality, assume that i1 = i3. Then
(i 1i 2)(i 3i 4) = (i 1i 4i 2)  G. Case 3: All four of the integers, i1, i2, i3, and i4 are distinct. Then
(i 1i 2)(i 3i 4) = (i 1i 3i 2)(i 1i 3i 4)  G.
Definition 8: A group G is said to be simple if G has no nontrivial normal subgroups. Equivalently, G is simple if the only normal subgroups N of G are N = G and N = {1}.
By Lagrange's theorem, if G = Zp, p a prime, then G is simple. On the other hand, if G = Zn, n  1, nor prime, then G is not simple. For if p is prime dividing n, then N = {0, p, 2p,..., (n - 1) · p} is a nontrivial normal subgroup of G. 1, nor prime, then G is not simple. For if p is prime dividing n, then N = {0, p, 2p,..., (n - 1) · p} is a nontrivial normal subgroup of G.
Another example of a simple group is given by the following important result.
Theorem 9 (Abel): Assume that n  4. Then An is simple. 4. Then An is simple.
In order to prove this result, we require
Lemma 10: Let N be a normal subgroup of An (n > 5). If N contains a 3-cycle, then N = An.
Proof: By Proposition 7, it suffices to show that every 3-cycle belongs to N. Let (ijk)  N and let (i'j'k') be an arbitrary 3-cycle. Let N and let (i'j'k') be an arbitrary 3-cycle. Let   Sn be any permutation having the property Sn be any permutation having the property
 (i) = i',
 (j) = j',
 (k) = k'.
Then
(4)
 (ijk)  -1 -1 = (i'j'k').
If   An, then (4) asserts that (i'j'k') An, then (4) asserts that (i'j'k')  N since N is normal. Therefore assume that N since N is normal. Therefore assume that  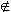 An. Since n > 5, there exist integers a, a' (1 < a, a' < n) such that An. Since n > 5, there exist integers a, a' (1 < a, a' < n) such that
{a, a'}  {i', j', k'} =  .
Then, since  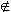 An, An, 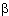 = (aa') = (aa')  An. However, An. However,
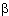 (ijk) 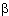 -1 -1 = (aa')  (ijk)  -1 -1(aa')
= (aa')(i'j'k')(aa')
= (i'j'k').
Thus, again (i'j'k')  N, so N = An and the lemma is proved. N, so N = An and the lemma is proved.
Proof of Theorem 9: An has order 1,1,3 for n = 1,2,3 respectively. In these cases, An has no proper subgroups by Lagrange's theorem. Thus, let us now assume that n > 5. Let N 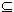 An be a normal subgroup N An be a normal subgroup N  {1}. We must show that N = An. By Lemma 10 it suffices to show that N contains a 3-cycle. For each {1}. We must show that N = An. By Lemma 10 it suffices to show that N contains a 3-cycle. For each  Sn, let f( Sn, let f( ) = the number of integers j (1 < j < n) such that ) = the number of integers j (1 < j < n) such that  (j) = j. Let us choose (j) = j. Let us choose   N - {1} for which f( N - {1} for which f( ) is a maximum. Since ) is a maximum. Since   1, f( 1, f( ) < n - 1. However, if ) < n - 1. However, if  (j) = j for n - 1 values of j then (j) = j for n - 1 values of j then  = 1, so that f( = 1, so that f( ) < n - 2. If f( ) < n - 2. If f( ) = n - 2, then ) = n - 2, then  is a transposition, which contradicts the fact that is a transposition, which contradicts the fact that   An. Therefore, f( An. Therefore, f( ) < n - 3. We assert that f( ) < n - 3. We assert that f( ) = n - 3. Assume the contrary. Then f( ) = n - 3. Assume the contrary. Then f( ) < n - 4, and there are at least four integers not mapped into themselves by ) < n - 4, and there are at least four integers not mapped into themselves by  . Let us examine the expression of . Let us examine the expression of  as the product of nontrivial disjoint cycles. There are two possibilities. Either there exists an r-cycle (r > 3) in the expression or only transpositions occur. In the former case, as the product of nontrivial disjoint cycles. There are two possibilities. Either there exists an r-cycle (r > 3) in the expression or only transpositions occur. In the former case,  looks like looks like
(5)
(i1i2i3...)...,
while in the later  is of the form is of the form
(6)
(i1i2)(i3i4)...
In the first case, if f( ) = n - 4, then ) = n - 4, then  is a 4-cycle, which contradicts the fact that is a 4-cycle, which contradicts the fact that  is even. Therefore, in the first case, f( is even. Therefore, in the first case, f( ) < n - 5. Therefore, there exist integers i4, i5 (1 < i1, i5 < n), distinct from i1, i2, i3, and not left fixed by ) < n - 5. Therefore, there exist integers i4, i5 (1 < i1, i5 < n), distinct from i1, i2, i3, and not left fixed by  . Let . Let  = (i3i4i5). Then = (i3i4i5). Then
and any integer left fixed by  is also left fixed by is also left fixed by  '. Since N is normal, we have '. Since N is normal, we have  ' '  N. Moreover, N. Moreover,   ' '  1, so that f( 1, so that f(  ') < f( ') < f( ) by the definition of ) by the definition of  . But . But   '-1 leaves fixed all integers which are not left fixed by '-1 leaves fixed all integers which are not left fixed by  and and   '-1 leaves i2 fixed as well. Therefore, f( '-1 leaves i2 fixed as well. Therefore, f(  '-1) < f( '-1) < f( ) + 1. Thus, a contradiction is reached if ) + 1. Thus, a contradiction is reached if  is of the form (5). Assume that is of the form (5). Assume that  is of the form (6). Let i5 be an integer left fixed by is of the form (6). Let i5 be an integer left fixed by  and set and set  = (i3i4i5). Then = (i3i4i5). Then
is an element of N, which leaves every integer left fixed by  , except for i5. Moreover, , except for i5. Moreover,    ', so that ', so that   '-1 '-1  1. Further 1. Further   '-1 leaves fixed the f( '-1 leaves fixed the f( ) - 1 integers which are left fixed both by ) - 1 integers which are left fixed both by  and and  ' and it leaves i1 and i2 fixed as well. Therefore, ' and it leaves i1 and i2 fixed as well. Therefore,   '-1 leaves f( '-1 leaves f( ) + 1 integers fixed, which is a contradiction to the choice of ) + 1 integers fixed, which is a contradiction to the choice of  . We have finally proved that the assumption f( . We have finally proved that the assumption f( ) < n - 4 leads to a contradiction, and therefore f( ) < n - 4 leads to a contradiction, and therefore f( ) = n - 3. But then there are exactly three integers not left fixed by ) = n - 3. But then there are exactly three integers not left fixed by  , so , so  is a 3-cycle. Thus, N contains a 3-cycle as claimed. is a 3-cycle. Thus, N contains a 3-cycle as claimed.
|
 :G1
:G1 G2
G2 (a · b) =
(a · b) =  (a) ·
(a) ·  (b) (a,b
(b) (a,b  G1 if
G1 if  is also surjective G1 is isomorphic to G2).
is also surjective G1 is isomorphic to G2).
 :G1
:G1 G2
G2 (a · b) =
(a · b) =  (a) ·
(a) ·  (b) (a,b
(b) (a,b  G1 if
G1 if  is also surjective G1 is isomorphic to G2).
Let H be a subgroup of G. If for every
is also surjective G1 is isomorphic to G2).
Let H be a subgroup of G. If for every  G,
G, H is a homomorphism, then
H is a homomorphism, then  H is a homomorphism, then
H is a homomorphism, then  im(f)
im(f) .
. =
= 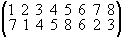
 = (172)(3458),
= (172)(3458), = (i1i2...ir)(j1...js)(k1...kt)...
= (i1i2...ir)(j1...js)(k1...kt)... = (i1ir)(i1ir-1)...(i1i2)(j1js)...(j1j2)(k1kt)...(k1k2)...
= (i1ir)(i1ir-1)...(i1i2)(j1js)...(j1j2)(k1kt)...(k1k2)... ) = (r-1) + (s-1) + (t-1) + ...,
) = (r-1) + (s-1) + (t-1) + ...,
 ,
, 
 Sn.
Sn.
 )
)  N(
N( ) + N(
) + N( )
) =
=  1...
1... a,
a,  =
=  1...
1... b
b

 )
)  (N(
(N( 1)+N(
1)+N( 2)+...+N(
2)+...+N( a)) +
a)) +  1)+...+N(
1)+...+N( b)) (mod 2)
b)) (mod 2) N(
N( ) + N(
) + N( ) (mod 2).
) (mod 2). = (jii2...ir)(j1...js)(k1...kt)...
= (jii2...ir)(j1...js)(k1...kt)...
 ) = 1 + N(
) = 1 + N( ) = N(
) = N( ) + N(
) + N( ).
). = (jj2...jsii2...ir)(k1...kt)...
= (jj2...jsii2...ir)(k1...kt)...
 ) = (r + s -1) + (t - 1)+... = N(
) = (r + s -1) + (t - 1)+... = N( ) + N(
) + N( ).
). = (ii2...ik-1)(jik+1...ir)(j1...js)(k1...kt)...
= (ii2...ik-1)(jik+1...ir)(j1...js)(k1...kt)...
 ) = (k - 2) + (r - k) + (s - 1) + (t - 1) + ...
) = (k - 2) + (r - k) + (s - 1) + (t - 1) + ... ) + N(
) + N( ) - 2
) - 2 N(
N( ) + N(
) + N( ) (mod 2).
) (mod 2). )
)  N(
N( 1 + ... + N(
1 + ... + N( a) (mod 2)
a) (mod 2) a (mod 2),
a (mod 2), : Sn
: Sn  Z2
Z2 (
( ) = N(
) = N( ) (mod 2).
) (mod 2). G.
G. G.
G. G.
G. (i) = i',
(i) = i', (j) = j',
(j) = j', (k) = k'.
(k) = k'. (ijk)
(ijk) -1 = (i'j'k').
-1 = (i'j'k'). {i', j', k'} =
{i', j', k'} =  .
. (ijk)
(ijk) -1 = (aa')
-1 = (aa') (ijk)
(ijk) -1(aa')
-1(aa') ' =
' = 

 -1 = (i1i2i4...)...,
-1 = (i1i2i4...)..., ' =
' = 

 -1 = (i1i2)(i4i5)...
-1 = (i1i2)(i4i5)...