 1 (mod p).
1 (mod p). 1 (mod p).
1 (mod p). G
G| Back | Table of Contents |
|
|
Sylow's TheoremsWe now come to the three theorems of Sylow, which are among the most important results in the study of finite groups. Recall that earlier we proved Lagrange's theorem, which asserts that if G is a finite group and H is a subgroup of G, then H divides the order of G. Note, however, that the converse of Lagrange's theorem is false. That is, if G has order n and if m|n, then there does not necessarily exist a subgroup of G of order m. For example, A4 is a group of order 12 which has no subgroups of order 6. Sylow's theorem comes about as close as one can come to providing a converse to Lagrange's theorem. Throughout this section, let G be a group of order n, let p be a prime dividing n, and let Definition 1: A subgroup of G of order pa is called a p-Sylow subgroup. Our main results are the following theorems of the Norwegian mathematician Sylow, which we will denote SI, SII, and SII. Theorem 2 (SI): G contains a p-Sylow subgroup.
Theorem 3 (SII): If P and Q are any two p-Sylow subgroups of G, then there exists
Theorem 4 (SIII): Suppose that G has r p-Sylow subgroups. Then r|n and In order to prove these remarkable results, a number of preliminaries must be introduced. If G is any group, then the center of G, denoted ZG, is defined as
ZG = {g
 G | gx = xg for all x G | gx = xg for all x  G}. G}.
Then If S is any subset of G, then the normalizer of S, denoted
NG(S) = {g
 G |gSg-1 G |gSg-1 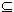 S}. S}.
Then NG(S) < G. Moreover, if S is a subgroup of G, then Let
C = {xgx-1 | x
 G}. G}.Moreover, if C1,...,Ch are conjugacy classes of G, then
G = C1
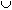 ... ...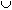 Ch Ch
and Ci
Proposition 5: Let
|NG(S)| = n/hg.
Proof: Let C denote the conjugacy class containing g,
G = g1NG(S)
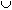 ... ... 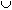 ghNG(S) ghNG(S)and (2)
giNG(S)
 gjNG(S) = gjNG(S) =  (i (i  j). j).
This will suffice to prove the proposition. For giNG(S) contains |NG(S)| elements for i = 1,...,h and by (2), none of these sets overlap. Therefore, by (1),
x = gim = gjm'.
However,
NG(S) = {x
 G | xgx-1 = g} G | xgx-1 = g}
= {x
 G | xg = gx}. G | xg = gx}.
But, by (3), gj-1gi = m'm-1
gj-1gig = ggj-1gi
 giggi-1 = gjggj-1, giggi-1 = gjggj-1,
which contradicts the choice of gi's. Thus (2) is proved. Let
gi-1xgx-1gi = g
 (gi-1x)g(gi-1x)-1 = g (gi-1x)g(gi-1x)-1 = g gi-1x gi-1x  NG(S) NG(S) x x  giNG(S). giNG(S).Thus (1) is proved. Let us now give proofs of the Sylow theorems. Proof of SI: The result is clearly true if Case A: p|(|ZG|). In this case, by Proposition 7 of the section on abelian groups, ZG contains an element x of order p. Let Case B: p Case C: |ZG| = n0 or 1. Let C1,...,Ct denote the conjugacy classes of G. Note that
n = |ZG| + |Cs+1| + ... + |Ct|
 n n  n0 or 1 (mod p) n0 or 1 (mod p) n0 or 1 n0 or 1  0 (mod p) (since p|n). 0 (mod p) (since p|n).
But Proof of SII: Let S1 and S2 be two p-Sylow subgroups of G, and let
G = S1g1S2
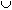 ... ... 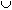 S1gtS2 S1gtS2
be the decomposition of G relative to the two subgroups S1 and S2. Then since
n =
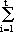 (pa · pa)/ui, (pa · pa)/ui,
where ui = the order of
n0 =
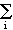 pa/ui. pa/ui.
Since Ui < S2,
gi-1S1gi
 S2. S2.But both gi-1S1gi and S2 have order pa, so that we conclude that
gi-1S1gi = S2.
Corollary 6: Let S be a p-Sylow subgroup of G. Then S is the only p-Sylow subgroup of G if and only if Proof:
Proposition 7: Let S be a p-Sylow subgroup of G, Proof: Let
G = g1N
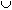 g2N g2N 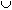 ... ... 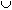 giN, t = [G:N] giN, t = [G:N]be a coset decomposition. Then (4)
g1Sg1-1,g2Sg2-1,...,giSgi-1
are p-Sylow subgroups of G. These are distinct, since if
giSgi-1 = gjSgj-1,
we see that Proof of SIII: Let t be the number of p-Sylow subgroups of G. Then, by Proposition 7,
G = Sg1N
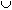 Sg2N Sg2N 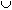 ... ... 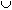 SgvN SgvN
be the decomposition of G with respect to the two subgroups S and N. Without loss of generality, assume that
n = pan0 =
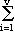 par/ci par/ci
where
n0 = r
(5)
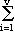 1/ci = m0 1/ci = m0 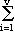 pa/ci pa/ci
= m0(1 +
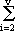 pa/ci) pa/ci) n0/m0 = 1 + n0/m0 = 1 + 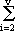 pa/ci pa/ci t = n/r = 1 + t = n/r = 1 + 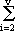 pa/ci pa/ci
Note that since Let us now give a few examples of applications of the Sylow theorems.
Proposition 8: Let p and q be distinct primes, Proof: By the fundamental theorem of abelian groups, it suffices to show that G is abelian. Let P and Q, be respectively a p-Sylow and a q-Sylow subgroup of G. Since every element of P except the identity has order p and every element of Q except the identity has order q, we see that Thus, for example, since Example 1: No group of order 20 is simple. Let G be a group of order 20. The number of 5-Sylow subgroups is one of 1,2,4,5,10,20. However, the number of 5-Sylow subgroups is congruent to 1(mod 5), so that this number is 1. Thus, if P is the unique 5-Sylow subgroup, then |
| Back | Table of Contents |