 B
B B
B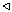 G
G(1) HK < G.
(2) H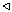 HK; H
HK; H K
K 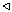 K.
K.
(3) HK/H K/H
K/H  K.
K.
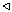 G,
G, G,
G, G/H.
G/H. H is a homomorphism. The kernel of f is ker(f) = {x
H is a homomorphism. The kernel of f is ker(f) = {x  G | f(x) = 1H}.
A function
G | f(x) = 1H}.
A function  B
B B
B A
A H is a homomorphism, then
H is a homomorphism, then  im(f)
im(f) :G1
:G1 G2
G2 (a · b) =
(a · b) =  (a) ·
(a) ·  (b) (a,b
(b) (a,b  G1).
G1).
| Back | Table of Contents |
|
|
The Isomorphism Theorems of Group TheoryPreviously we proved the first isomorphism theorem of group theory. Let us now complement our previous result with two additional isomorphism theorems which actually follow from the first. Throughout the following sections on group theory the following notation will be in effect: G is a group; if H is a subgroup, then we will write Let Let H be a subgroup of G such that (1)
G > H > K.
Since
(hK)(h'K)-1 = hh'-1K
 H/K, H/K,so that H/K is a subgroup of G/K. Thus, we have described a procedure for constructing subgroups of G/K.
Proposition 1: Let Proof: Set
H = {g
 G | gK G | gK  H}. H}.
If
hh'-1K = (hK)(h'K)-1
 H, H,
since H is a subgroup of G/K. Therefore,
Proposition 2: Let
Theorem 3 (Second Isomorphism Theorem): Let
(G/K)/(H/K)
 G/H. G/H.Proof: By Proposition 2,
G
 G/K G/K
G/K
 (G/K)/(H/K). (G/K)/(H/K).Since i and j are surjective, the homomorphism
ji:G
 (G/K)/(H/K) = M (G/K)/(H/K) = Mis surjective. Moreover, (3)
ker(j) = H/K.
Note that if  j(i(g)) = 1M j(i(g)) = 1M g g  i-1(H/K) = H. i-1(H/K) = H.
Therefore, Example 1: Let which can be easily verified directly. Throughout the remainder of this section, let H and K be subgroups of G. Recall that
Proposition 4: HK is a group if and only if Proof:
(hk)(h'k')-1 = h(kk'-1h'-1)
= hh''k''
 HK. HK.Therefore, HK is a subgroup of G. Corollary 5: If one of H, K is a normal subgroup of G, then HK is a subgroup of G. Proof: Assume that Let us now suppose that 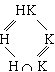
Theorem 6 (Third Isomorphism Theorem): Assume that (1) HK < G. (2) H (3) HK/H Proof: We have already proved (1) and (2). In order to prove (3), let us consider the homomorphisms
i:K
 HK, HK,
j:HK
 HK/H, HK/H,defined by
i(k) = k (k
 K), K),
j = the natural homomorphism.
Note that i is an injection, so that
ji:K
 HK/H. HK/H.
Then it is clear that
(ji)(k) = hkH.
Indeed, since
hkH = k(k-1hk)H = kH.
But Example 2: Let a result which can be trivially checked. Let H and K be subgroups of a finite group G. As for our last result in this section, let us compute the number of elements in the set HK. If
|HK| =
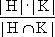 If H is not a normal subgroup of G, then HK is not necessarily a group. However, we will prove that (4) still holds in this case. Even is HK is not a group, it still makes sense to consider the set of right cosets H\HK. A typical coset belonging to H\HK is Hhk, where
|H\HK| =
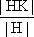 . .Similarly, (6)
|H
 K\K| = K\K| =  . .Thus, to prove (4), it suffices to prove that (7)
|H\HK| = |H
 K\K| K\K|Let us define a function  : H\HK : H\HK H H K\K K\Kby  (Hhk) = (H (Hhk) = (H K)k, h K)k, h  H, k H, k  K. K.
(H
 K)k = (H K)k = (H K)hk' = (H K)hk' = (H K)k', K)k',  (Hhk) = (Hhk) =  (Hh'k'), (Hh'k'),  is well defined. is well defined.
If |
| Back | Table of Contents |