 B
B B
B A
A B
B B
B A
A :G1
:G1 G2
G2 (a · b) =
(a · b) =  (a) ·
(a) ·  (b) (a,b
(b) (a,b  G1).
A function
G1).
A function  B
B G,
G,
 .
. H,
H, H.
H. G)
G)| Back | Table of Contents |
|
|
HomomorphismsRecall that an isomorphism f from a group G into a group H is a function
f(g · g') = f(g) · f(g')
for all
Definition 1: Let G and H be groups. A function Note that the product We noted that isomorphic systems are essentially the same, being "abstractly equal". This is certainly not true of homomorphic systems in general. A homomorphic image can be compared to a silhouette of a system projected or mapped onto a screen. Certain features like the profile are preserved, but certain features such as coloration are lost. Example 1: An isomorphism Example 2: Let
f(g) = 1H.
for all Example 3: Let
f(FaRb) = Fa
To prove that (1) holds, we must show that (2)
f([FaRb] · [FcRd]) = f(FaRb) · f(FcRd).
However, we showed earlier that
[FaRb] · [FcRd] = Fa+cRb+d if c = 0,
and
[FaRb] · [FcRd] = Fa+cRd-b if c = 1.
Therefore, the left-hand side of (2) equals Fa+c in both cases, and (3)
Fa+c = f(FaRb) · f(FcRd),
which proves (2). Thus, f is a homomorphism. Example 4: Let f :Z
f(a) = 2a (a
 Z). Z).
Since
f(a + b) = 2(a + b) = 2a + 2b = f(a) + f(b),
we see that f is a homomorphism. Example 5: We may generalize Example 4 as follows: Let G be an abelian group, and let n be an integer. Then let us define
fn(a) = an (a
 G). G).Since
fn(ab) = (ab)n = anbn = fn(a)fn(b),
we see that fn is a homomorphism.
Proposition 2: let (1) f(1G) = 1H. (2) f(a-1) = f(a)-1 (a (3) If K is a subgroup of G, then f(K) is a subgroup of H. Proof: (1) Since 1G· 1G= 1G and since f is an isomorphism, we see that
f(1G) = f(1G· 1G) = f(1G)· f(1G).
Multiplying both sides by f(1G)-1, we get (2) It suffices to show that (4)
f(a-1)·f(a) = f(a)f(a-1) = 1H.
For then by the uniqueness of inverses in H, we have
a-1a = a·a-1 = 1G.
Therefore, by part (1) and the fact that f is a homomorphism, we get (4). (3) By Proposition 2 of the section on subgroups, it suffices to show that if Suppose that f:G
ker(f) = {x
 G | f(x) = 1H}. G | f(x) = 1H}.
We will call ker(f) the kernel of f. If F is an isomorphism, then  H is a homomorphism, then H is a homomorphism, then
Proposition 3: If f:G Proof: First let us show that ker(f) is a subgroup of G. Let
a,b
 ker(f) ker(f)  f(a) = f(b) = 1H f(a) = f(b) = 1H f(a) = f(b-1) = 1H (by part (2) of proposition 2 above.) f(a) = f(b-1) = 1H (by part (2) of proposition 2 above.) f(a · b-1) = f(a) f(b-1) = 1H f(a · b-1) = f(a) f(b-1) = 1H a · b-1 a · b-1  ker(f). ker(f).
Let us now show that ker(f) is normal. Let
f(axa-1) = f(a) · f(x) · f(a)-1
= f(a) · 1H· f(a)-1
=1H,
so that axa-1 If one knows the kernel of a homomorphism, then one has a good deal of information about the homomorphism, as the next two results show. Let f :G H be a homomorphism, H be a homomorphism,  H. H. G G
Proposition 4: Let f :G
f -1(h) = g · ker(f).
Proof: If
f(g') = f(g · k) = f(g) f(k)
= f(g) [since k
 ker(f)] ker(f)]
= h.
Therefore,
f(g'·g-1) = 1H
 g'·g-1 g'·g-1  ker(f) ker(f) g' g'  g · ker(f) g · ker(f)
Thus,
Corollary 5: Let Proof:
Proposition 3 tells us that with every homomorphism f of G into a group H there is an associated normal subgroup of G, ker(f). Conversely, suppose that we are given a normal subgroup N of G. Then there is an associated homomorphism, which we will now construct. We have already defined the quotient group G/N. Let us associate to N the homomorphism
iN:G
 G/N, G/N,
iN(g) = gN.
Indeed, iN is a homomorphism since
iN(g1g2) = g1g2N
= g1N · g2N
= iN(g1)iN(g2) (g1,g2
 G) G)by the definition of multiplication in G/N
Proposition 6: The homomorphism Proof: It is clear that iN is surjective. Moreover,
g
 ker(iN ker(iN 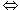 iN(g) = 1G/N iN(g) = 1G/N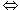 gN = N gN = N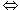 g g  N. N.Therefore, ker(iN) = N. The homomorphism Suppose that G, H, and J are groups, and suppose that 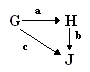
We see from the diagram that there are two homomorphisms defined from G into J, ba and c. If Let 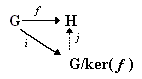
Here i is the canonical homomorphism iker(f). A common sort of question which arises in many contexts is: Does there exist a homomorphism
Theorem 7 (1st [or fundamental] Isomorphism Theorem): Let Remarks: 1. In many books, the first isomorphism theorem consists of the statement that if f :G
2. The real utility of Theorem 7 (as well as the other isomorphism theorems) is that they allow one to conclude that two groups are isomorphic to one another without actually constructing the isomorphism. Thus, these isomorphism theorems allow one to build a calculus for computing with groups. 3. The fundamental theorem asserts that G/ker(f) can be identified with the image of f under the isomorphism of j. Moreover, once this identification is carried out, the commutativity of the diagram implies that the homomorphism Example 6: Let Example 7: Let
f(Fa· Rb) = Fa.
Then f is surjective and Proof of Theorem: Let
j(gK) = f(g).
Therefore, if j exists, it is unique and must be given by (6). Let us try to define j by (6). First, we must check that the definition of j(gK) depends only on the coset gK and not on the choice of g. But if
j(gK·g'K) = j(gg'K) = f(gg') = f(g)f(g')
= j(gK)j(g'K).
Finally, j is an isomorphism, since if |
| Back | Table of Contents |