|
Examples of Groups
As was mentioned in the introduction to this section, a general theory is not of much value unless there are some interesting examples to which the theory applies. In this sense, the theory of groups is a superb theory. Let us now survey some various examples of groups which naturally present themselves in various branches of mathematics.
Examples from Arithmetic
Many of the arithmetic systems which we studied in the chapter on sets were groups, even though we did not call attention to this fact at that time.
Example 1: G = Z, with respect to the binary operation of addition. As mentioned in the last section, the identity element is 0 and the inverse of x is -x.
Example 2: G = Q, the rational numbers, with respect to the binary operation of addition. The identity element is 0 and the inverse of a/b is (-a)/b.
Example 3: G = Q - {0}, with respect to the binary operation of multiplication of rational numbers. Since the product of two nonzero rational numbers is a nonzero rational number, multiplication does, indeed, define a binary operation on Q - {0}. The identity element is the rational number 1, and the inverse of the rational number a/b 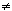 0 is b/a, since (a/b)(b/a) = 1. 0 is b/a, since (a/b)(b/a) = 1.
Example 4: G = N, with respect to the binary operation
of addition. This is not a group. Axioms G1 and G2 hold, but axiom G3 does not. For example, 1 has no inverse with respect to addition in N.
Example 5: G = Zn with respect
to the operation of addition of residue classes. The identity element is 0, since x + 0 = x + 0 = x and similarly 0 + x = x for all x  Zn. The inverse of x is -x, since x + -x = x + (-x) = 0 and similarly -x + x = 0. Note that Zn is a finite abelian group of order n. Zn. The inverse of x is -x, since x + -x = x + (-x) = 0 and similarly -x + x = 0. Note that Zn is a finite abelian group of order n.
Example 6: G = Zxn with respect
to the operation of multiplication of residue classes. We saw in the earlier section on congruences that multiplication of residue classes is actually a binary operation on Zxn - that is, the product of two elements of Zxn is again an element of Zxn. The identity element is 1. if a  Zxn, then a has an inverse with respect to multiplication by proposition 4 of the section on congruences .Therefore, G is a group. Moreover, by the discussion in the section on congruences, Zxn is a finite abelian group of order Zxn, then a has an inverse with respect to multiplication by proposition 4 of the section on congruences .Therefore, G is a group. Moreover, by the discussion in the section on congruences, Zxn is a finite abelian group of order  (n), where (n), where
 (n) denotes Euler's function. (n) denotes Euler's function.
The Symmetric Groups
In the section on Historical Perspectives we introduced the symmetric group Sn in connection with the solution of equations in radicals. Recall that Sn consists of all permutations
where {i1,i2,...,in} is some rearrangement of {1,2,...,n}. It is clear that a permutation is just a function  from {1,2,...,n} into {1,2,...,n} - that function defined by from {1,2,...,n} into {1,2,...,n} - that function defined by
 (1) = i 1.
 (2) = i 2.
.
.
.
 (n) = i n.
Moreover, since {i1,...,in} is a rearrangement of {1,2,...,n}, it is clear that  is one to one and onto - that is, is one to one and onto - that is,  is a bijection. Conversely, every bijection of {1,2,...,n} onto itself defines a permutation. This gives us a clue how to define the product of two permutations is a bijection. Conversely, every bijection of {1,2,...,n} onto itself defines a permutation. This gives us a clue how to define the product of two permutations  and and 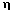 . The product . The product  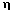 must be a bijection of {1,2,...,n} onto itself. Let it be the function defined by composition: must be a bijection of {1,2,...,n} onto itself. Let it be the function defined by composition:
(1)
Thus, the product  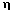 is the permutation gotten by first performing the permutation is the permutation gotten by first performing the permutation 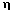 and following it by the permutation and following it by the permutation  . It is easy to compute products of permutations. For example, let us compute the product of . It is easy to compute products of permutations. For example, let us compute the product of 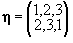 , and , and 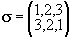 . First, . First,  maps 1 into 3 and maps 1 into 3 and 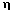 maps 3 into 1. Therefore, maps 3 into 1. Therefore, 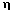  maps 1 into 1. Since maps 1 into 1. Since  maps 2 into 2 and maps 2 into 2 and 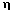 maps 2 into 3, the product maps 2 into 3, the product 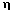  maps 2 into 3. Similarly, maps 2 into 3. Similarly, 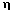  maps 3 into 2. Thus maps 3 into 2. Thus 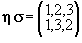 . .
Since the composition of functions is associative, we see that multiplication of permutations is associative. Moreover, the permutation 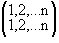 is an identity with respect to multiplication of permutations. Finally if is an identity with respect to multiplication of permutations. Finally if 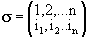 , then , then  has an inverse with respect to multiplication. Indeed if we set has an inverse with respect to multiplication. Indeed if we set 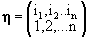 , then it is reasonably easy to see that , then it is reasonably easy to see that
so that 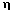 is an inverse for is an inverse for  . Thus, we have proved that Sn is a group. Note, however that Sn is not usually abelian. For example, . Thus, we have proved that Sn is a group. Note, however that Sn is not usually abelian. For example,
By induction, it is easy to see that the order of Sn equals 1·2·3·...·n = n! (read "n factorial"). Also, its easy to see that the inverse of   Sn is just the inverse of Sn is just the inverse of  considered as a bijection from {1,2,...,n} onto itself. considered as a bijection from {1,2,...,n} onto itself.
The last comment suggests a generalization of the symmetric group Sn. Let A be an arbitrary set, and let SA denote the set of bijections of A onto itself. Then SA can be made into a group by defining multiplication in SA via (gf)(x) = g(f(x)), for f,g  SA, x SA, x  A. The identity element is the identity function on A, and the inverse of the bijection f is the function f -1. SA is called the symmetric group on the set A, and the elements of SA are called permutations of A. If A = {1,2,...,n}, then SA = Sn. A. The identity element is the identity function on A, and the inverse of the bijection f is the function f -1. SA is called the symmetric group on the set A, and the elements of SA are called permutations of A. If A = {1,2,...,n}, then SA = Sn.
Examples from Geometry
Example 7: Let
R2 = R × R = {(x,y) | x,y  R R},
R3 = R × R × R = {(x,y,z) | x,y,z  R R}.
Then R2 is called the Euclidean plane and R3 is called Euclidean 3 - space. The sets R2 and R3 may be visualized as the usual plane and three-dimensional spaces of analytic geometry, respectively. The groups which we consider will consist of various motions of R2 and R3. For the moment, let us confine ourselves to R2.
A motion of R2 is a bijection of R2 onto itself; that is, a motion of R2 is just a permutation of R2. A motion of R2 is what was classically called a "transformation." From our study of symmetric groups, we know that the set of all motions of R2 forms a group under the operation of composition of functions. This group will be denoted by M(R2). Most motions of R2 are uninteresting. However, many geometric situations give rise to interesting collections of motions which form groups under the operation of multiplication of permutations. It is useful to think of a motion A of R2 as moving the point (x,y) to the point A((x,y)). The product of A · B of the two motions A and B moves the point (x,y) to the point A(B((x,y))) - that is, taking the product of A · B amounts to first performing the motion B, then the motion A.
Example 8: A linear motion of R2 is one which moves the point (x,y) to the point (x',y'), where
(2)
x' = ax + by,
y' = cx + dy.
and ad - bc 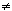 0. The last condition guarantees that for every (x',y') there exists a unique (x,y) which satisfies the system of equations (2). For if (x,y) satisfies (2) for a given (x',y'), then by multiplying the first equation by d and the second by b, and then subtracting the second from the first, we see that dx'-by' = (ad-bc)x, and thus, since ad-bc 0. The last condition guarantees that for every (x',y') there exists a unique (x,y) which satisfies the system of equations (2). For if (x,y) satisfies (2) for a given (x',y'), then by multiplying the first equation by d and the second by b, and then subtracting the second from the first, we see that dx'-by' = (ad-bc)x, and thus, since ad-bc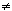 0, we have 0, we have
(3)
x = (d/(ad - bc))x' + (-b/(ad - bc))y'.
Similarly,
(3')
y = (-c/(ad - bc))x' + (a/(ad - bc))y'.
If A' denotes the linear motion which maps (x',y') into (x'',y''), where
x'' = a' x' + b' y',
y'' = c' x' + d' y'.
then A' · A maps (x,y) into (x'',y''), where
x'' = (a'a + b'c)x + (a'b + b'd)y,
x'' = (c'a + d'c)x + (c'b + d'd)y.
Moreover,
(a'a + b'c)(c'b + d'd)-(c'a + dc')(a'b + b'd)=(ad - bc)(a'c' - b'c')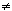 0. 0.
Therefore, A' · A is a linear motion. The identity motion is clearly a linear motion and the inverse of the linear motion A is described by formulas (3) and (3'). Thus, the set of linear motions of R2 forms a group, called the two-dimensional general linear group, denoted GL(2,R).
Example 9: A translation of R2 is a motion which moves the point (x,y) to the point (x',y'), where
(4)
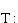 x'= x + a, y' = y + b
We can visualize a translation as moving the whole plane along the vector whose initial point is the origin and whose terminal point is (a,b) (Figure 1).
Figure 1: A Translation in R2.
The product T1 · T2 of the two translations
is the translation
The identity motion is clearly a translation and the inverse of the translation
is the translation
The set of translations of R2 forms a group, denoted T(R2). The translation (4) will be denoted by Ta,b.
Example 10: The motion of R2 obtained from the following linear motion M by a translation Ta,b is called an affine motion of R2. If M corresponds to
then the affine motion Ta,b· M moves the point (x,y) to the point (x',y'), where
x' = 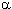 x + 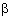 y + a,
y' = 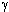 x + 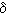 y + b.
The set of affine motions of R2 forms a group, denoted A(R2). We will leave the verification of the group axioms to the reader. to see the results of an affine motion click here.
Thus far, all our examples of the groups of motions have been infinite. But many interesting finite groups occur as groups of motions. Let us give some examples.
Example 11: A rigid motion of R2 is a motion of R2 which preserves distances between points. Recall from analytic geometry that the distance between two points (x,y) and (x',y') is given by
{(x - x')2 + (y - y')2}1/2.
An example of a rigid motion of R2 is the motion which rotates the plane through an angle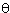 . This motion will be denoted R . This motion will be denoted R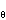 . Another example is the translation Ta,b. . Another example is the translation Ta,b.
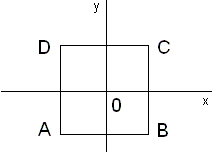
Let S 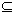 R2 be any subset. A symmetry of S is a rigid motion which maps S onto itself. At first this may seem like a strange definition, but it really does coincide with our intuitive concept of symmetry. Let us consider an example. Let S be a square, centered at the origin, as in Figure 2. R2 be any subset. A symmetry of S is a rigid motion which maps S onto itself. At first this may seem like a strange definition, but it really does coincide with our intuitive concept of symmetry. Let us consider an example. Let S be a square, centered at the origin, as in Figure 2.
Figure 2: A Square with Labeled Vertices.
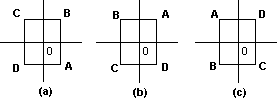
The identity motion I is clearly a symmetry of the square. Let R be the motion of rotation counterclockwise though an angle 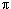 /2. The square of Figure 2 is mapped onto itself situated as shown in Figure 3(a). Therefore, R is a symmetry of the square. Similarly, R · R = R2 and R · R · R = R3 are symmetries. (R2 is just a counterclockwise rotation through an angle of /2. The square of Figure 2 is mapped onto itself situated as shown in Figure 3(a). Therefore, R is a symmetry of the square. Similarly, R · R = R2 and R · R · R = R3 are symmetries. (R2 is just a counterclockwise rotation through an angle of 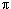 , while R3 is just a counterclockwise rotation through an angle of 3 , while R3 is just a counterclockwise rotation through an angle of 3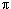 /2.) Note, however, that R4 brings the square back to its original position, since R4 is a counterclockwise rotation through 2 /2.) Note, however, that R4 brings the square back to its original position, since R4 is a counterclockwise rotation through 2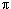 . Therefore, R4 = I. . Therefore, R4 = I.
Figure 3: Symmetries of a Square.
Another symmetry of the square can be gotten by rotating the square around the X-axis, resulting in the configuration of Figure 4. Let us call this symmetry F (for "flip"). Then it is clear that upon repeating F twice, the square is returned to its original position. Therefore, F2 = I. Moreover, a trivial calculation shows that R · F = F · R3.
By combining flips and rotations, we get symmetries of the form
(5)
I, F, R, R2, R3, F · R, F · R2, F · R3
It might seem that this list should go on to include many other symmetries, say F · R3 · F. However, since R · F = FR3, R4 = I,, F2 = I, we see that
F · R3 · F = R · F · F = R
With a little patience, one can show that the product of any two of the elements (5) is another element of the form (5), and that the elements of (5) form a group. We have assembled the multiplication for the group in Table 1. (Tables of this type are also referred to as Cayley tables)
Table 1
Multiplication Table for the Group of Symmetries of the Square
|
I |
R |
R2 |
R3 |
F |
FR |
FR2 |
FR3 |
| I |
I |
R |
R2 |
R3 |
F |
FR |
FR2 |
FR3 |
| R |
R |
R2 |
R3 |
I |
FR3 |
F |
FR |
FR2 |
| R2 |
R2 |
R3 |
I |
R |
FR2 |
FR3 |
F |
FR |
| R3 |
R3 |
I |
R |
R2 |
FR |
FR2 |
FR3 |
F |
| F |
F |
FR |
FR2 |
FR3 |
I |
R |
R2 |
R3 |
| FR |
FR |
FR2 |
FR3 |
F |
R3 |
I |
R |
R2 |
| FR2 |
FR2 |
FR3 |
F |
FR |
R2 |
R3 |
I |
R |
| FR3 |
FR3 |
F |
FR |
FR2 |
R |
R2 |
R3 |
I |
If, in this table, we look up element a on the row index and b on the column
index, the tabular entry gives the value of a · b. You are strongly
encouraged to verify the entries in the table, using the same reasoning as used above. The table can easily be used to check that every element has an inverse. Thus, once the table is derived, it is easy to verify that the elements form a group. Note that in this case, the associativity is guaranteed, since permutations are functions, the group operations is compositions of functions and composition of functions is associative.
The group which we have constructed is the group of symmetries of the square. It is a group of order 8. There are symmetries of the square which have not yet been mentioned. For example, the symmetry gotten by rotating the square about the Y-axis; or about the line y = x; or about the line y = -x. The reader should have no problem verifying that these symmetries can be expressed in terms of products of powers of F and R, and are therefore in the group we constructed. Note that he group of symmetries of the square is nonabelian. Indeed, we have
R · F = F · R -1 = F · R 3 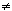 F · R.
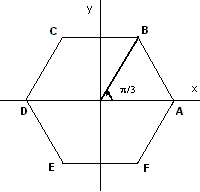
Example 12: Let us generalize the preceding example. Let n > 2 be a positive integer, and let Pn be a regular polygon of n sides with one of its vertices on the X-axis.(Figure 5.)
Figure 5: P6
This last requirement is actually unnecessary but will make our exposition easier. We will construct the group of symmetries of Pn. Two obvious symmetries are suggested by Example 11. Let R denote a counterclockwise rotation through an angle of 2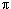 /n, and let F denote a rotation about the X-axis. It is then simple to check that R and F satisfy the following relations: /n, and let F denote a rotation about the X-axis. It is then simple to check that R and F satisfy the following relations:
Rn = I, F2 = I,
R · F · R = F,
where I denotes the identity symmetry. As in Example 11, we can show that the product of any two elements
I, R, R2,..., Rn-1, F, F·R, F·R2,..., F·Rn-1
is again and element of the same form. Of course, in this example, things are slightly more complicated, so let us outline a more efficient analysis than given in Example 11. First note that since Rn-1·R = Rn = I, we have R-1 = Rn-1, where we have used the uniqueness of the inverse. Therefore, we see that the relation R·F·R = F is equivalent to R·F = F·R-1 = F·Rn-1. Therefore, if a is any positive integer,
Ra·F = F·Ra(n-1).
Let us now consider the product of two elements Fa·Rb and Fc·Rd, where a, b, c, and d are positive integers. Without loss of generality, we may assume that
0 < a, c < 1, 0 < b, d < n - 1.
Then if c = 0,
Fa·Rb·Fc·Rd = Fa·(Rb·F)·Rd = Fa·F·Rb(n-1)+d
= Fa+c·Rd-b.
Therefore, we have proved closure under multiplication. We leave the verification of the remaining group axioms to the reader. The group which is defined in the preceding discussion is called the dihedral group and is denoted Dn. In particular, if n=4, D4 is the group of symmetries of the square. Note that Dn always contains 2n elements.
Example 13: We can speak of symmetries of subsets of R3 by taking over piecemeal the definitions for R2. The three-dimensional analogues of the dihedral groups are gotten by looking at the symmetries of regular solids. In high school geometry it is proved that there are only five regular solids - the tetrahedron, the cube, the octahedron, the dodecahedron, and the icosahedron. Their groups of symmetries are very complicated.
Examples from Analysis
Example 14: Let 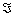 denote the set of all functions f : R denote the set of all functions f : R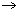 R. Define the sum of two functions f,g R. Define the sum of two functions f,g   the be the function f + g defined by the be the function f + g defined by
( f + g)(x) = f(x) + g(x) (x  R R).
With respect to the operation +,  becomes an abelian group. The identity element is the zero function 0 defined by becomes an abelian group. The identity element is the zero function 0 defined by
0(x) = 0 (x  R R).
The inverse of the function f is the function -f defined by
(- f)(x) = - f(x) (x  R R).
Example 15: Let C  denote the set of all continuous functions. Since the sum of continuous functions is a continuous function, we see that if f,g denote the set of all continuous functions. Since the sum of continuous functions is a continuous function, we see that if f,g  C, then f + g C, then f + g  C. Therefore, the operation + defined in Example 14 also defines a binary operation on C. With respect to this binary operation, C becomes an abelian group. C. Therefore, the operation + defined in Example 14 also defines a binary operation on C. With respect to this binary operation, C becomes an abelian group.
Miscellaneous Examples
Example 16: We may put a group structure R2 as follows. Define a binary operation called addition on R2 setting (a,b) + (c,d) = (a+c, b+d), where a + c, b + d denote the sums of a,c and b,d as real numbers. The identity element of R2 with respect to this binary operation is (0,0), and the inverse element of (a,b) is (-a,-b). The reader should have no difficulty in verifying these assertions.
Example 17: This example provides us with a method for manufacturing new groups from given ones. Let G and G' be groups, and let G × G' denote the Cartesian product of G and G'. Let us define a binary operation on G × G' by setting (g,g')·(h,h') = (gh, g'h'). Then it is easy to see that this binary operation is associative. An identity element is (1G,1G'), and the inverse of (g,g') is just (g-1,g'-1). The group G × G' is called the direct product of G and G'. If G = G' = R, then G × G' is just the group of Example 16.
|
 G, we have
G, we have
 G, we have
G, we have
 G.
G. G,
G, G
G Zxn.
Zxn. Zxn
Zxn Z}.
Z}. G.
G.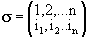
 (1) = i1.
(1) = i1.
 (2) = i2.
(2) = i2.
 (n) = in.
(n) = in.

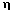 (i) =
(i) =
 (
(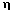 (i)).
(i)).

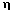 =
= 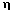
 =
= 
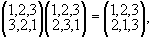
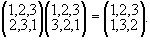
 0.
0.
 x'= x + a,
x'= x + a,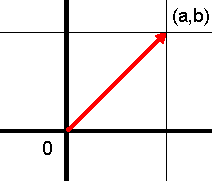
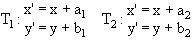
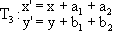
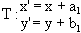
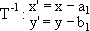
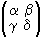
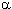 x +
x + 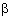 y + a,
y + a,
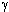 x +
x + 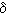 y + b.
y + b.
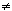 F · R.
F · R.
 R).
R). R).
R).
 R).
R).