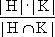
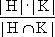 If H is a subgroup of G then
If H is a subgroup of G then | Back | Table of Contents |
|
|
Decomposition with Respect to Two SubgroupsEarlier we discovered that we could decompose a group G into (right or left) cosets with respect to a subgroup H. In this section we will generalize this decomposition to a decomposition of G with respect to two subgroups, H and K. The decomposition derived in this section was first discovered by Frobenius at the end of the nineteenth century and will be very useful in our discussion of the Sylow theorems. Throughout this section, let G be a group and let H and K be subgroups of G. Let us define an equivalence relation ~ on G as follows: Say that ~ is reflexive: g = 1 · g · 1 ~ is symmetric: g ~ g'
(h
 H, k H, k  K) K)  g' = h-1gk-1 g' = h-1gk-1  g' ~ g. g' ~ g.~ is transitive: g ~ g', g' ~ g"
(h,h'
 H; k H; k  K) K)  g = (hh')g"(k'k) g = (hh')g"(k'k)  g ~ g". g ~ g".Thus, ~ is an equivalence relation on G and therefore decomposes G into equivalence classes Ci
Ci = HgiK.
Thus, (1)
G =
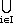 HgiK. HgiK.
Moreover, since
HgiK
 HgjK = HgjK =  (i (i j) j)We will be interested in the case where G is a finite group of order n. Suppose that there are t equivalence classes C1,...,Ct. Then (1) may be written (3)
G = Hg1K
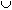 ... ... 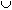 HgtK. HgtK.Therefore, by (2) and (3), (4)
|G| = |Hg1K| + ... + |HgtK|.
Now it is clear that (5)
|HgiK| = |gi-1HgiK|,
since if HgiK = {x1,...,xa}, then
|HgiK| = |HiK|.
By equation (4) of the section on isomorphism theorems, we see that (7)
|HiK| =
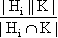 = = 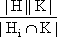 . .Therefore, by (6) and (7), we have (8)
|HgiK| =
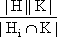 . . By combining (4) and (8), we may summarize our results as follows: Theorem 1 (Frobenius): Let G be a finite group of order n, let H and K be subgroups of order p and q, respectively, and let g1,...,gt be representatives of the equivalence classes with respect to ~. Then
n =

where If in Theorem 1, we set |
| Back | Table of Contents |