 H
H G
G H
H G
G H is a homomorphism. The kernel of f is ker(f) = {x
H is a homomorphism. The kernel of f is ker(f) = {x  G | f(x) = 1H}.
Let G1 and G2 be groups. An isomorphism from G1 to G2 is an injection
G | f(x) = 1H}.
Let G1 and G2 be groups. An isomorphism from G1 to G2 is an injection  :G1
:G1 G2
G2 (a · b) =
(a · b) =  (a) ·
(a) ·  (b) (a,b
(b) (a,b  G1 if
G1 if  is also surjective G1 is isomorphic to G2).
A function
is also surjective G1 is isomorphic to G2).
A function  B
B B
B B
B A
A| Back | Table of Contents |
|
|
Cayley's TheoremWe have stated that on of the main objectives of group theory is to write down a complete list of non-isomorphic groups. At first, such a task appears hopeless. For, as we have seen, groups pop up in some very unexpected places and, therefore, if we set out to compile a list of all non-isomorphic groups, we would hardly begin to know where to look. The following theorem of Cayley solves this dilemma. Theorem 1: Every group is isomorphic to a subgroup of a permutation group Proof: Let G be a group, 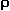 g:G g:G  G G
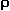 g(x) = xg-1 (x g(x) = xg-1 (x  G). G).
If
G
 SG SG
defined by (1)
g
 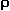 g g
Since What Cayley's theorem tells us is that permutation groups and their subgroups are all the groups that can exist. Unfortunately, the problem of classifying the subgroups of a permutation group is extremely complicated, even in the case of a finite permutation group. Therefore, Cayley's theorem does not allow us to easily identify a complete list of groups. The above argument actually proves somewhat more than claimed. For if G is finite, having order n, then G is isomorphic to a subgroup of SG. Therefore we have
Corollary 2: If G has finite order n, then G is isomorphic to a subgroup of Sn.
|
| Back | Table of Contents |