The Fundamental Theorem of Abelian Groups

Earlier we mentioned a broad goal of the theory of finite groups is to arrive at a classification of all finite groups. In this section we will achieve a much more modest goal: We will classify all finite abelian groups. Our main result will be the fundamental theorem of abelian groups (FT), which asserts that a finite abelian group is isomorphic to a direct product of cyclic groups. We will be able to pin down the structure of a finite abelian group further by specifying to some extent the cyclic groups which occur.

Theorem 1 (FT): Let G be a finite abelian group. Then G is isomorphic to a direct product of cyclic subgroups.

Proof: Suppose that G has order n. The theorem is clear if n = 1. Thus, we may assume that n > 1, and we may proceed by induction on n. Let x₀ be an element of G of highest order, and let C₀ = [x₀]. Since G is abelian, C₀ G. Moreover, G/C₀ has order less than n, so the induction hypothesis implies that there exist cyclic subgroups H₁,H₂,...,H_s of G/C₀ such that

G/C₀ H₁ H₂ ... H_s.

Each H_i is of the form C_i/C₀, where C_i is a subgroup of G which contains C₀. Since H_i is cyclic, H_i = [x_iC₀] for some x_i G. Let us prove that

(2)

G [x₀] [x₁,...x_s].

for some choice of x_i such that H_i = [x_iC₀]. Let us apply Theorem 3 of the section on direct products. Since G is abelian, every element of [x₀] commutes with every element of [x₁,...,x_s]. If g G, then gC₀ G/C₀, so that by (1),

Thus,

for some c₀ C₀. But c₀ = s₀^a₀ since C₀ = [x₀]. Therefore,

and g is the product of an element of [x₀] and an element of [x₁...x_s]. In order to apply Theorem 3 of the section on direct products, we must prove that

[x₀] [x₁,...,x_s] = {1}.

This is the heart of the proof. Let a_i denote the order of x_i. Let us first show the order of x_iC₀ (in G/C₀) is also a_i. Let b_i denote the order of x_iC₀. Since (x_iC₀)^a_i = x_i^a_iC₀ = C₀, we see that

Since (x_iC₀)^b_i = C₀, we see that x_i^b_i C₀, so that x_i^b_i = x₀^c for some integer c > 0. Since the order of x_iC₀ is the same as the order of x_ix₀^dC₀, and since x_ix₀^dC₀ is a generator of H_i, we may replace x_i by x_ix₀^d for any integer d. In doing so, we replace c + b_id. By choosing d appropriately, we can guarantee that 0 < c + b_id < b_i. Thus, without loss of generality, we may assume that

The order of x_i^b_i is a_i/(b_ia_i) = a_i/b_i [by(4)]. The order of x₀^c is r/(r,c), where r = the order of x₀. Therefore, by (5),

On the other hand, since x₀ has maximal order in G, a_i < r. Therefore,

If c > 0, then (r,c) < c and thus we have

which contradicts (5). Therefore, c = 0 and x_i^b_i = x₀⁰ = 1. Thus a_i|b_i, which together with (4) implies that a_i = b_i. We have thus proved that the order of x_iC₀ is a_i. Every element in G/C₀is of the form

(x₁C₀)^₁...(x_sC₀)^_s = x_1¹...x_s^sC₀,   0 < _i < a_i.

By what we have proved above, H_i = C_i/C₀ has order a_i, so that by (1), G/C₀ has order a₁a₂...a_s. Therefore, all the elements of (6) are distinct. In particular, if x_1¹...x_s^s C₀ (0 < _i < a_i), then ₁ = ... = _s = 0. Let us finally prove (3). If g [x₀] [x₁,...,x_s], then g = x_1¹...x_s^s (0 < _i < a_i) and g C₀. Therefore, as we have shown above, ₁ = ... = _s = 0, and g = 1. Thus, (3) is proved and with it (2). However, by induction,

[x₁,...,x_s] [y₁] ... [y_t],

so that by (2),

G [x₁] [y₁] [y_t],

and G is a direct product of cyclic groups.

Corollary 2: Let G be a finite abelian group. Then there exist positive integers n₁,...,n_t such that

G Z_n1 ... Z_nt.

Proof: Every cyclic group is isomorphic to Z_n for some positive integer n.

Corollary 3: Let G be a finite abelian group. Then there exists a set of prime powers ,,..., (not necessarily distinct) such that

G Z Z ... Z.

Proof: Let n₁,...n_t be as in Corollary 2, and let

n_i = 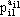... 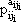 (1 < i < t).

Then by Corollary 5 of the section on direct products,

G Z Z ... Z ... Z.

Note that H K K H with respect to the mapping : H K K H defined by (h,k) = (k,h) (h H, k K). Therefore, we may rearrange factors in a direct product and still get a group isomorphic to the original one. Using this fact, we can normalize the decomposition of Corollary 3 as follows: Let q₁,...,q_v be the distinct primes among {p₁,...,p_s}, arranged so that

Let

be the powers of the prime q_i (not necessarily distinct) appearing in the decomposition of Corollary 3, arranged so that

Define

G(q_i) = Z Z ....

Then Corollary 3 and the above remark imply that

G G(q₁) G(q₂) ...  G(q_v).

It is clear that every element of G(q_i) has order a power of q_i. Moreover, from (9), we see that the set of all element of G(q₁ ... G(q_v) whose order is a power of q_i is {1} {1} ... G(q_i) ... {1} G(q_i). Thus, we have

Corollary 4: Let H(q_i) denote the subgroup of G consisting of all elements whose order is a power of q_i. Then

H(q_i) Z ... Z

and

G H(q_i) ... H(q_v).

If q is a prime, then H(q) is called the q-primary part of G. Let us consider an example. Let G = Z₁₀ Z₂₅. Then

Z₁₀ Z₂ Z₅,   Z₂₅ = Z_5².

Therefore,

G Z₂ Z₅ Z_5².

The 2-primary part of G is Z₂, while the 5-primary part of G is Z₅ Z_5².

Definition 5: The prime powers

are called the elementary divisors of G.

It is clear that if we are given the elementary divisors of G, then it is possible to determine G up to isomorphism using (9).

Theorem 6: The elementary divisors of G are uniquely determined by G. In other words, the decomposition (9) of G is unique.

Proof: The primes q₁,...,q_v are uniquely determined as the distinct primes dividing the order of G. Let 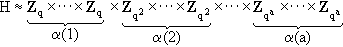q = q_i for some i and let H = the q-primary part of G. Then H depends only on q and G. Suppose that we are given a decomposition of H of the form

It suffices to show that 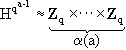(1), (2),...,(a) depend only on G and q. If b is a positive integer, then set H^b = {h^b | h H}. Note that q^cZ_q^b = {0} if c > b, Z_q^b-c if c < b. Thus,

so that order of H^qa-1 is q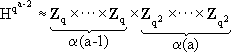^(a). Thus, (a) is determined only by G, q, and a. Next note that

Thus, the order of H^qa-2 is

q^(a-1)+2(a).

Thus, (a - 1) depends only on G, q, and a - 1. Proceeding in this way, we see that (1),...,(a) are determined uniquely by G and q.

Example 1: Let us determine up to isomorphism all abelian groups of order 16. Since 16 = 2⁴, the possible sets of elementary divisors are

(a) 2⁴.

(b) 2, 2³.

(c) 2, 2, 2².

(d) 2, 2, 2, 2.

(e) 2², 2².

The corresponding abelian groups are

(a) Z₁₆.

(b) Z₂ Z₈.

(c) Z₂ Z₂ Z₄.

(d) Z₂ Z₂ Z₂ Z₂.

(e) Z₄ Z₄.

None of the groups (a)-(e) are isomorphic to one another by Theorem 6. This example suggests the following generalization. Let p be a prime, m a positive integer. Let us determine the abelian groups of order p^m. We know that every such groups is uniquely specified by its elementary divisors

where

The last property comes from the fact that

Z_p^a1 Z_p^a2 ... Z_p^as

has order p^a₁·p^a₂...p^a_s. Thus, to each abelian group of order p^m is associated the set {a₁,...,a_s} of positive integers such that a₁ + ... + a_s = m, a₁ < a₂ < ... < a_s. Such a set is called a partition of m. Conversely, to each partition {a₁,...,a_s} of m there corresponds an abelian group of order p^m - the group (10). Moreover, by Theorem 6, distinct partitions of m correspond to nonisomorphic groups. Let p(m) denote the number of distinct partitions of m. Then, we see that the number of nonisomorphic abelian groups of order p^m is p(m).

In the above example, p = 2, m = 4. The partitions of 4 are

Thus, there are five nonisomorphic abelian groups of order 2⁴, as we discovered.

We proved earlier that the number of nonisomorphic groups of order n is at most nⁿ². If n = p^m, there are at most p^mp2m. How does this number compare with the number of nonisomorphic abelian groups of order p^m? In other words, how big is p(m)?

The problem of determining the law of growth of the partition function p(m) has been solved completely, but only in the twentieth century, and belongs to a chapter of contemporary mathematics called additive number theory. Although many results about partitions had been discovered as early as the eighteenth century by Euler and Lagrange, it was not until the invention of the circle method by Hardy and Ramanujan in 1918 that any real progress was made in determining the order of magnitude of p(m). Hardy and Ramanujan proved that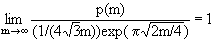

In other words, for large m, p(m) is approximately equal to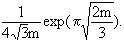

We leave it to the reader to demonstrate the this quantity is much smaller that p^mp2m, in the sense that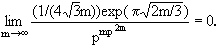

The proof of (11) is very difficult and relies on analysis. Much more precise results than (11) are known. In fact in 1936 Rademacher found a beautiful exact formula for p(m) in terms of an infinite series.

Let us close this section with a very simple, but useful application of the fundamental theorem.

Proposition 7: Let G be an abelian group whose order is divisible by a prime p. Then G contains an element of order p.

Proof: Without loss of generality assume G to be of the form

Z_p^a1 Z_p^a2 ... Z_p^at Z_p^b1 ....

Then

has order p.