|
Solution of Equations in Radicals
In this section we return to a subject touched upon in the introduction, the solution of equations in radicals.
Let f = F[x] be a nonconstant polynomial
f = Xn + aXn-1 + ... + an,
First, let us clarify what we mean when we ask for a "solution in radicals" of the equation f(x) = 0. Roughly speaking, we mean a set of formulas which express the zeros of f in terms of the coefficients a1,...,an using only addition, subtraction, multiplication, division, and extraction of roots. Let us reformulate this idea in terms of field extensions.
Definition 1: Let E be a field extension of F. We say that E is a radical extension of F if E = F( 1,..., 1,..., t), where t), where  1m1 1m1  F, F,  1m1 1m1  F( F( 1,..., 1,..., i-1) (i = 2,3,...,t) for some integers m1,m2,...,mt. i-1) (i = 2,3,...,t) for some integers m1,m2,...,mt.
Remark: In the definition of a radical extension, let m denote the least common multiple of m1, m2,...,mt Then for each i(1 < i < t), m = kimi for some positive integer ki. Therefore,
 im im = (  imi imi) ki  F(  1 1,...,  i-1 i-1) (i = 2,...,t).
Thus, if we replace each mi by m, we see that in the definition of a radical extension, we may assume that all mi are equal.
Roughly speaking, a radical extension of F is obtained by succesively adjoining a sequence of radical to F.
Let F = Q in all the following examples:
Example 1: E = Q( is a radical extension of Q. is a radical extension of Q.
Example 2: E = Q( , ,  ) is a radical extension of Q. ) is a radical extension of Q.
Example 3: E = Q( ), where ), where  is a primitive nth root of unity, is a radical extension of Q since 1 = is a primitive nth root of unity, is a radical extension of Q since 1 =  n n  Q. Q.
Definition 2: We say that f is solvable in radicals if the splitting field Ef of f over F is contained in some radical extension E of F.
The reader should have no difficulty convincing himself that the definition of solvability in radicals coincides with the roughly stated notion which we previously introduced. For indeed, if Ef = F( 1,..., 1,..., n), where n), where  1,..., 1,..., n are the zeros of f. Therefore, to say that Ef is contained in some radical extension of F just means that the zeros n are the zeros of f. Therefore, to say that Ef is contained in some radical extension of F just means that the zeros  i can be expressed in terms of radicals and in addition, subtraction, multiplication, and division. i can be expressed in terms of radicals and in addition, subtraction, multiplication, and division.
Proposition 3: Let E/F be a radical extension. Then E is contained in a radical extension E' of F such that E'/F is a Galois extension.
Proof: Let E = F( 1,..., 1,..., n), where n), where  1m1 1m1  F, F,  1m1 1m1  F( F( 1,..., 1,..., i-1) ( i = 2,...,t ). Set i-1) ( i = 2,...,t ). Set  imi = ai and let for each i(1 < i < t), aij(1 < j < ki) be the conjugates of ai over F. Let E' be the smallest subfield of F containing F and all the zeros of the polynomials Xmi - aij (1 < i < t, 1 < j < ki). It is clear that E' is normal over F and hence E'/F is a Galois extension (since E' is a splitting field). Moreover, it is clear that E' imi = ai and let for each i(1 < i < t), aij(1 < j < ki) be the conjugates of ai over F. Let E' be the smallest subfield of F containing F and all the zeros of the polynomials Xmi - aij (1 < i < t, 1 < j < ki). It is clear that E' is normal over F and hence E'/F is a Galois extension (since E' is a splitting field). Moreover, it is clear that E'  E, since for some j, aij = ai hence ai E, since for some j, aij = ai hence ai  E' (1 < i < t). Finally, E' is a radical extension of F. E' (1 < i < t). Finally, E' is a radical extension of F.
Let us now investigate the properties of the Galois group of a radical extension E/F. Our main result is
Theorem 4: Let E/F be a radical Galois extension with Galois group G. Then G is a solvable group.
Proof: Let us utilize the preceding Remark and write E = F( 1,..., 1,..., t) where t) where  1n 1n  F, F,  in in  F( F( 1,..., 1,..., i-1) (i = 2,...,t). Let i-1) (i = 2,...,t). Let  be a primitive nth root of unity and let E' = E( be a primitive nth root of unity and let E' = E( ). Since E/F is a Galois extension, E is obtained from F by adjoining all roots of a finite collection of polynomials belonging to F[X]. In order to get E' from E, we adjoin all roots of the polynomial Xn - 1 ). Since E/F is a Galois extension, E is obtained from F by adjoining all roots of a finite collection of polynomials belonging to F[X]. In order to get E' from E, we adjoin all roots of the polynomial Xn - 1  F[X]. Therefore, E' is obtained by adjoining to F all the roots of a finite collection of polynomials belonging to F[X], and hence E'/F is a Galois extension. Let H = Gal(E'/F), and set F[X]. Therefore, E' is obtained by adjoining to F all the roots of a finite collection of polynomials belonging to F[X], and hence E'/F is a Galois extension. Let H = Gal(E'/F), and set
E 0 = F, E 1 = F(  ),
E i = F(  ,  1 1,...,  i-1 i-1) (i = 2,...,t+1).
Then
(1)
F = E 0  ...  E t+1 = E'.
By the fundamental theorem of Galois theory, to the chain of intermediate fields (1), there corresponds a chain of subgroups of H:
(2)
H = H 0  H 1  ...  H i+1 = {1},
where Hi = Gal(E'/Ei). Let us show that the chain (2) of subgroups of H is a normal series with abelian factors. Indeed, E1 is the splitting field over E0 of the polynomial Xn - 1. Therefore, E1/E0 is a Galois extension with abelian Galois group. Therefore, by Theorem 8 of the section of the fundamental theorem of Galois theory, H1 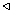 H0 and Gal(E1/E0) = H0/H1 is abelian. Next, note that Ei(i > 1) contains the nth roots of unity and Ei+1 = Ei( H0 and Gal(E1/E0) = H0/H1 is abelian. Next, note that Ei(i > 1) contains the nth roots of unity and Ei+1 = Ei( i), where i), where  i is a zero of Xn - ai, where ai = i is a zero of Xn - ai, where ai =  in in  Ei.
By Example 5 of the section on the Galois group of a polynomial, Ei+1/Ei(i > 1) is a Galois extension with abelian Galois group. Therefore, by Theorem 8 of the section on the fundamental theorem of Galois theory, Hi+1 Ei.
By Example 5 of the section on the Galois group of a polynomial, Ei+1/Ei(i > 1) is a Galois extension with abelian Galois group. Therefore, by Theorem 8 of the section on the fundamental theorem of Galois theory, Hi+1 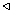 Hi and Gal(Ei+1/Ei) = Hi/Hi+1 (i = 1,2,...,t) is abelian. Thus we have proved that (2) is a normal series for H having abelian factors. Therefore, H is a solvable group. It is no easy to show that G is solvable. We have Hi and Gal(Ei+1/Ei) = Hi/Hi+1 (i = 1,2,...,t) is abelian. Thus we have proved that (2) is a normal series for H having abelian factors. Therefore, H is a solvable group. It is no easy to show that G is solvable. We have
F  E  E', G = Gal(E/F), H = Gal(E'/F).
Let J = Gal(E'/E). By the fundamental theorem of Galois theory, J < H. But E/F is a Galois extension, so that by Theorem 8 of the section on the fundamental theorem, J 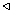 H and G = Gal(E/F) = H/J. But then G is a quotient of the solvable group H and hence is solvable by Corollary 9 of the section on solvable groups. H and G = Gal(E/F) = H/J. But then G is a quotient of the solvable group H and hence is solvable by Corollary 9 of the section on solvable groups.
Corollary 5: Let f  F[X] be a nonconstant polynomial. If f is solvable by radicals, then GalF( f ) is solvable. F[X] be a nonconstant polynomial. If f is solvable by radicals, then GalF( f ) is solvable.
Proof: If f is solvable in radicals, then there exists a radical extension E of F such that
F  E f  E.
Without loss of generality, by Proposition 3, we may assume that E/F is a Galois extension. Let H = Gal(E/F). Since Ef /F is a normal extension, Ef /F is a Galois extension. Le G = Gal(E/Ef ). Then by Theorem 8 of the section on the fundamental theorem, we have G 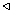 H and H and
GalF(f ) = Gal(Ef /F) = H/G.
But H is solvable by Theorem 4, so that H/G is solvable. Thus, GalF(f ) is solvable.
Corollary 6: There exist fifth-degree polynomials in Q[X] which are not solvable in radicals. Thus, the quintic (fifth-degree) equation has no general solution in radicals.
Proof: We saw in the section on the Galois group of a polynomial that f = X5 - 6X + 3 has the property that GalQ( f ) = S5. If f is solvable in radicals, then, by Corollary 5, S5 is solvable. But Since A5 is a simple group (Theorem 9 of symmetric groups) a composition series for S5 is given by
S 5  A 5  {1},
and the factors are
S 5/A 5 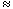 Z2 Z2, A 5/{1} 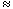 A 5.
But A5 is nonabelian, so that S5 is not solvable. Therefore, f is not solvable in radicals.
We have seen that if a polynomial f is solvable in radicals, then GalF(f ) is solvable. In the remaining part of this section we will prove the converse. Actually we will accomplish considerably more. If GalF(f ) is solvable, we will actually give a method for constructing a radical extension containing Ef . In particular, this will lead us to an expression of the zeros of f in terms of radicals. When the procedure of this section is applied to polynomials of degrees 2,3,or 4 we will get the formulas which were mentioned in the introduction. In order to carry out our program, it will be necessary to study in some detail the structure of a Galois extension E/F of prime degree p where F contains the pth roots of unity. Our main result will be
Theorem 7: Let F be a field and let E/F be a Galois extension of prime degree p. Assume that F contains the pth roots of unity. Then there exists a  F such that E = F( F such that E = F( ), where ), where  is a zero of Xp - a. is a zero of Xp - a.
The proof of Theorem 7 is accomplished via a trick going back to Lagrange. Let  be a primitive pth root of unity, be a primitive pth root of unity,  an arbitrary pth root of unity. Then an arbitrary pth root of unity. Then  is of the form is of the form  a (a = 0,1,...,p - 1). Let a (a = 0,1,...,p - 1). Let   E. Since E/F is a Galois extension of prime order p, Gal(E/F) is cyclic of degree p. Let E. Since E/F is a Galois extension of prime order p, Gal(E/F) is cyclic of degree p. Let  be a generator of Gal(E/F). Then be a generator of Gal(E/F). Then
Gal(E/F) = {1,  ,  2 2, ...,  p-1 p-1}.
Let us define the Lagrange resolvent < , , > by > by
It is clear that < , , > >  E. We may restate Theorem 7 as follows: E. We may restate Theorem 7 as follows:
Theorem 8: Let F be a field and let E/F be a Galois extension of prime degree p. Assume that F contains the pth roots of unity, and let   E - F. Then there exists a pth root of unity E - F. Then there exists a pth root of unity  such that such that
(1) < , , >p >p  F, F,
(2) E = F(< , , >). >).
It is clear that Theorem 8 implies Theorem 7, upon setting a = < , , >p. >p.
Proof: First, let us show that a least one of the Lagrange resolvents < a, a, > (a = 1,...,p - 1) is nonzero. Let us assume the contrary. Then > (a = 1,...,p - 1) is nonzero. Let us assume the contrary. Then
(3)
If  is a primitive pth root of unity, then is a primitive pth root of unity, then
0 =  p p - 1 = (  - 1)(  p-1 p-1 +  p-2 p-2 + ... + 1)
Let 0 < v < p - 1, v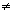 1 and set 1 and set  = =  v-1. Then v-1. Then  is a primitive pth root of unity, so that by (4), is a primitive pth root of unity, so that by (4),
Therefore, by (3),
(5)
Note that
<1,  > =  +   +  2 2 + ... +  p-1 p-1 .
Therefore,
= <1,  >,
and thus  a<1, a<1, > = <1, > = <1, > (a = 1,...,p - 1), so that <1, > (a = 1,...,p - 1), so that <1, > is left fixed by every element of Gal(E/F). We therefore deduce from the fundamental theorem of Galois theory, that <1, > is left fixed by every element of Gal(E/F). We therefore deduce from the fundamental theorem of Galois theory, that <1, > >  F. But, by (5), this implies that F. But, by (5), this implies that    F. And every element of F is invariant under F. And every element of F is invariant under  -1, so that -1, so that  = =    F. But this contradicts the hypothesis that F. But this contradicts the hypothesis that   E - F. Finally, we can conclude that at least one of the Lagrange resolvents < E - F. Finally, we can conclude that at least one of the Lagrange resolvents < a, a, > (a = 1,...,p - 1) is nonzero. Let > (a = 1,...,p - 1) is nonzero. Let  = =  a, where 1 < a < p - 1 is chosen so that < a, where 1 < a < p - 1 is chosen so that < , , > >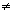 0. 0.
Let us now calculate the effect of  on < on < , , >. From the definition of < >. From the definition of < , , >, we have >, we have
where we have used the fact that   F and therefore F and therefore  ( ( ) = ) =  . Therefore, since . Therefore, since  p = 1, p = 1,
so that < , , >p is left fixed by all elements of Gal(E/F) = {1, >p is left fixed by all elements of Gal(E/F) = {1, ,..., ,..., p-1}. But this implies that < p-1}. But this implies that < , , >p >p  F, hence (1) holds. F, hence (1) holds.
Since  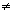 1, 1,  < < , , > = > =  -1< -1< , , > > 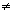 < < , , >. Therefore, < >. Therefore, < , , > is not left fixed by > is not left fixed by  , and < , and < , , > > 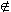 F by the fundamental theorem of Galois theory. Thus, F(< F by the fundamental theorem of Galois theory. Thus, F(< , , >) >) 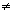 F. But, since deg(E/F = p, a prime, and F F. But, since deg(E/F = p, a prime, and F  F(< F(< , , >) >)  E, we see that deg(F(< E, we see that deg(F(< , , >)/F) = 1 or p. In the former case, F(< >)/F) = 1 or p. In the former case, F(< , , >) = F, which is a contradiction. Therefore, deg(F(< >) = F, which is a contradiction. Therefore, deg(F(< , , >)/F) = p, from which it follows that deg(E/F(< >)/F) = p, from which it follows that deg(E/F(< , , >)) = 1, and thus E = F(< >)) = 1, and thus E = F(< , , >). >).
Let us apply Theorem 7 to prove
Theorem 9: Let f  F[X] be a nonconstant polynomial such that GalF(f ) is solvable. Then f is solvable in radicals. F[X] be a nonconstant polynomial such that GalF(f ) is solvable. Then f is solvable in radicals.
Proof: Let deg(Ef /F) = n and let  be a primitive nth root of unity. Set Ef( be a primitive nth root of unity. Set Ef( ) = E', F( ) = E', F( ) = F'. The relationship between the fields Ef, F, E', and F' is illustrated in figure 2, where a line connecting the two fields denotes a containment relation. It suffices to show that E'/F is a radical extension. For then, since F ) = F'. The relationship between the fields Ef, F, E', and F' is illustrated in figure 2, where a line connecting the two fields denotes a containment relation. It suffices to show that E'/F is a radical extension. For then, since F  Ef Ef  E', we see that f is solvable in radicals. Note that E' is obtained from F by adjoining all zeros of f and Xn - 1, and thus E'/F is a Galois extension. Let G = Gal(E'/F) and let H be the subgroup of G corresponding to Ef under the Galois correspondence. Then Gal(E'/Ef ) = H. Moreover, since Ef /F is a Galois extension, H E', we see that f is solvable in radicals. Note that E' is obtained from F by adjoining all zeros of f and Xn - 1, and thus E'/F is a Galois extension. Let G = Gal(E'/F) and let H be the subgroup of G corresponding to Ef under the Galois correspondence. Then Gal(E'/Ef ) = H. Moreover, since Ef /F is a Galois extension, H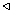 G and Gal(Ef /F) = G/H. But Gal(Ef /F) = GalF(f ) is solvable. Therefore, G/H is solvable. Moreover, by Example 5 of the section the Galois group of a polynomial, H = Gal(Ef( G and Gal(Ef /F) = G/H. But Gal(Ef /F) = GalF(f ) is solvable. Therefore, G/H is solvable. Moreover, by Example 5 of the section the Galois group of a polynomial, H = Gal(Ef( )/Ef ) is abelian and hence solvable. Thus, since H and G/H are solvable, G is solvable. Let J be the subgroup of G corresponding to F' under the Galois correspondence. Then J = Gal(E'/F') and J is a subgroup of a solvable group and hence is solvable. For the relationship between the various Galois groups we have defined, see Figure 2. )/Ef ) is abelian and hence solvable. Thus, since H and G/H are solvable, G is solvable. Let J be the subgroup of G corresponding to F' under the Galois correspondence. Then J = Gal(E'/F') and J is a subgroup of a solvable group and hence is solvable. For the relationship between the various Galois groups we have defined, see Figure 2.

Figure 2: The subfields of E' and their corresponding Galois Groups.
Since J is solvable, there exists a composition series
such that Ji/Ji+1 is a cyclic group of prime order pi (0 < i < t - 1). Let Fi be the fixed field of Ji. Then Ji = Gal(E'/Fi) and
Moreover, since Ji Ji+1, we see that Fi+1/Fi is a Galois extension with Galois group Ji/Ji+1. Thus, Fi+1/Fi is a Galois extension of prime degree pi. Let us now show that Fi contains the pith roots of unity. This will allow us to apply Theorem 7 to the extension Fi+1/Fi. Ji+1, we see that Fi+1/Fi is a Galois extension with Galois group Ji/Ji+1. Thus, Fi+1/Fi is a Galois extension of prime degree pi. Let us now show that Fi contains the pith roots of unity. This will allow us to apply Theorem 7 to the extension Fi+1/Fi.
If   Gal(E'/F'), then the restriction of Gal(E'/F'), then the restriction of  to E is an F-automorphism of E, that is, an element of Gal(E/F) [because E' = E( to E is an F-automorphism of E, that is, an element of Gal(E/F) [because E' = E( ), F' = F( ), F' = F( )]. Therefore, let us define the function )]. Therefore, let us define the function
 :Gal(E'/F')  Gal(E/F),
by  ( ( ) = the restriction of ) = the restriction of  to E ( to E (  Gal(E'/F')). It is trivial to check that Gal(E'/F')). It is trivial to check that  is an isomorphism. Therefore, J = Gal(E'/F') is isomorphic to a subgroup of G/H = Gal(Ef /F). In particular, since pi divides the order of J and since G/H has order n, we see that pi|n (0 < i < t - 1). If is an isomorphism. Therefore, J = Gal(E'/F') is isomorphic to a subgroup of G/H = Gal(Ef /F). In particular, since pi divides the order of J and since G/H has order n, we see that pi|n (0 < i < t - 1). If 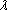 is a pith root of unity, then is a pith root of unity, then 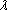 pi = 1, so that pi = 1, so that 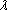 n = 1 (since pi|n). Therefore, every pith root of unity is an nth root of unity. But F' = F( n = 1 (since pi|n). Therefore, every pith root of unity is an nth root of unity. But F' = F( ) )  Fi (i = 0,...,t) and Fi (i = 0,...,t) and  is a primitive nth root of unity. Therefore, Fi (i = 1,...,t) contains the pith roots of unity, as asserted. is a primitive nth root of unity. Therefore, Fi (i = 1,...,t) contains the pith roots of unity, as asserted.
We may now apply Theorem 7 to each of the extensions Fi+1/Fi (0 < i < t - 1). We see that there exists  i+1 i+1  Fi+1 such that (1) Fi+1 = Fi( Fi+1 such that (1) Fi+1 = Fi( i+1) and (2) i+1) and (2)  i+1 is a zero of a polynomial of the form Xpi - ai+1 (ai+1 i+1 is a zero of a polynomial of the form Xpi - ai+1 (ai+1  Fi). Thus, we derive that Fi). Thus, we derive that
and
(1 < i < t - 1).
Thus, E' is a radical extension of F.
Theorem 10: Let f  F[X] be a nonconstant polynomial of degree at most 4. Then f is solvable in radicals. F[X] be a nonconstant polynomial of degree at most 4. Then f is solvable in radicals.
Proof: By Corollary 5 of the section on the Galois group of a polynomial, GalF(f ) is a subgroup of Sn (n < 4). Since a subgroup of a solvable subgroup is solvable, Theorem 9 implies that it suffices to show that S1, S2, S3 and S4 are solvable groups. This is obvious for S1 and S2 since these groups are abelian. A composition series for S3 is
S 3 A 3 {1}
and the composition factors are S3/A3  Z2, A3/{1} Z2, A3/{1}  Z3. Thus, S3 is solvable. A composition series for S4 is given by Z3. Thus, S3 is solvable. A composition series for S4 is given by
S 4 A 4 {(1),(12)(34),(13)(24),(14)(23)}  {(1),(12)(34)}  {1}.
The composition factors are isomorphic to
Z2, Z3, Z2, Z2.
Thus, S4 is solvable.
|
 1,...,
1,..., t),
t), 1m1
1m1  F,
F, 1m1
1m1  F(
F( 1,...,
1,..., i-1)
i-1) 1m1
1m1  F
F 
 1m = (
1m = ( 1m1)k1
1m1)k1  F,
F, imi
imi  F(
F( 1,...,
1,..., i-1)
i-1) 
 im = (
im = ( imi)ki
imi)ki  F(
F( 1,...,
1,..., i-1) (i = 2,...,t).
i-1) (i = 2,...,t). is a radical extension of Q.
is a radical extension of Q. ,
,  )
) ), where
), where  is a primitive nth root of unity, is a radical extension of Q since
is a primitive nth root of unity, is a radical extension of Q since  n
n  Q.
Q. 1,...,
1,..., n),
n), 1,...,
1,..., n are the zeros of f. Therefore, to say that Ef is contained in some radical extension of F just means that the zeros
n are the zeros of f. Therefore, to say that Ef is contained in some radical extension of F just means that the zeros  i can be expressed in terms of radicals and in addition, subtraction, multiplication, and division.
i can be expressed in terms of radicals and in addition, subtraction, multiplication, and division. 1,...,
1,..., n), where
n), where  1m1
1m1  F,
F, 1m1
1m1  F(
F( 1,...,
1,..., i-1)
i-1) imi = ai
imi = ai E,
E, E'
E' 1,...,
1,..., t)
t) 1n
1n  F,
F, in
in  F(
F( 1,...,
1,..., i-1)
i-1) be a primitive nth root of unity and let
be a primitive nth root of unity and let  ).
). F[X].
F[X]. ),
), ,
, 1,...,
1,..., i-1) (i = 2,...,t+1).
i-1) (i = 2,...,t+1). ...
...  Et+1 = E'.
Et+1 = E'. H1
H1  ...
...  Hi+1 = {1},
Hi+1 = {1}, H0
H0 i),
i), i is a zero of
i is a zero of  in
in  Ei.
Ei. Hi
Hi E
E  E', G = Gal(E/F), H = Gal(E'/F).
E', G = Gal(E/F), H = Gal(E'/F). H
H F[X]
F[X] Ef
Ef  E.
E. H
H A5
A5  {1},
{1}, Z2, A5/{1}
Z2, A5/{1}  A5.
A5. F
F ),
), is a zero of
is a zero of  be a primitive pth root of unity,
be a primitive pth root of unity,  an arbitrary pth root of unity. Then
an arbitrary pth root of unity. Then  is of the form
is of the form  a
a 
 E.
E. be a generator of
be a generator of  ,
,  2, ...,
2, ...,  p-1}.
p-1}. ,
, > by
> by ,
, > =
> =  +
+ 

 + ... +
+ ... +  p-1
p-1 p-1
p-1 .
. ,
, >
>  E.
E.
 E - F.
E - F. such that
such that ,
, >p
>p  F,
F, ,
, >).
>). ,
, >p.
>p. a,
a, >
> > =
> = 
 -a<
-a< a,
a, >
>
 -a
-a
 av
av v
v

 v
v

 (v-1)a.
(v-1)a. is a primitive pth root of unity, then
is a primitive pth root of unity, then p - 1 = (
p - 1 = ( - 1)(
- 1)( p-1 +
p-1 +  p-2 + ... + 1)
p-2 + ... + 1)
 p-1 +
p-1 +  p-2 + ... + 1 = 0.
p-2 + ... + 1 = 0.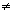 1
1 =
=  v-1.
v-1. is a primitive pth root of unity, so that by (4),
is a primitive pth root of unity, so that by (4),
 a =
a = 
 a(v-1) = 0.
a(v-1) = 0. > = p ·
> = p · 
 ,
,

 = p-1<1,
= p-1<1, >.
>. > =
> =  +
+ 
 +
+  2 + ... +
2 + ... +  p-1
p-1 .
. <1,
<1, > =
> = 
 +
+  2
2 + ... +
+ ... + 
 >,
>, a<1,
a<1, > = <1,
> = <1, >
> >
> >
>  F.
F.

 F.
F. -1, so that
-1, so that  =
= 

 F.
F.
 E - F.
E - F. a,
a, >
> =
=  a,
a, ,
, >
>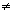 0.
0. on
on  ,
, >.
>. ,
, >,
>, <
< ,
, > =
> =  (
( +
+ 

 +
+  2
2 2
2 + ... +
+ ... +  p-1
p-1 p-1
p-1 )
)
 +
+ 
 2
2 +
+  2
2 3
3 + ... +
+ ... +  p-1
p-1 p
p
 -1(
-1(

 +
+  2
2 2
2 +
+  3
3 3
3 + ... +
+ ... +  p
p )
) -1<
-1< ,
, >,
>,
 F
F (
( ) =
) =  .
. p = 1,
p = 1, (<
(< ,
, >p) = <
>p) = < ,
, >p,
>p, ,
, >p
>p ,...,
,..., p-1}.
p-1}. ,
, >p
>p  F,
F,
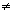 1,
1, <
< ,
, > =
> =  -1<
-1< ,
, >
> 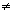 <
< ,
, >.
>. ,
, >
> , and
, and  ,
, >
> 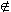 F
F ,
, >)
>) 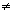 F.
F. F(<
F(< ,
, >)
>)  E,
E, ,
, >)/F) = 1
>)/F) = 1 ,
, >) = F,
>) = F, ,
, >)/F) = p,
>)/F) = p, ,
, >)) = 1,
>)) = 1, ,
, >).
>). F[X]
F[X] be a primitive nth root of unity. Set
be a primitive nth root of unity. Set  ) = E',
) = E', ) = F'. The relationship between the fields Ef, F, E', and F' is illustrated in figure 2, where a line connecting the two fields denotes a containment relation. It suffices to show that E'/F is a radical extension. For then, since
) = F'. The relationship between the fields Ef, F, E', and F' is illustrated in figure 2, where a line connecting the two fields denotes a containment relation. It suffices to show that E'/F is a radical extension. For then, since  Ef
Ef  E',
E',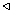 G
G )/Ef )
)/Ef )
 J1
J1  ...
...  Jt = {1}
Jt = {1} F1
F1  ...
...  Ft = E'.
Ft = E'. Ji+1,
Ji+1,
 Gal(E'/F'),
Gal(E'/F'), to E is an F-automorphism of E, that is, an element of
to E is an F-automorphism of E, that is, an element of  ),
), )].
)]. :Gal(E'/F')
:Gal(E'/F')  Gal(E/F),
Gal(E/F), (
( ) = the restriction of
) = the restriction of  to E
to E 
 Gal(E'/F')).
Gal(E'/F')). is an isomorphism. Therefore,
is an isomorphism. Therefore, 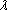 is a pith root of unity, then
is a pith root of unity, then 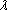 pi = 1,
pi = 1,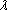 n = 1
n = 1 )
)  Fi
Fi is a primitive nth root of unity. Therefore, Fi
is a primitive nth root of unity. Therefore, Fi  i+1
i+1  Fi+1 such that (1)
Fi+1 such that (1)  i+1)
i+1) i+1 is a zero of a polynomial of the form
i+1 is a zero of a polynomial of the form  Fi).
Fi). ,
, 1,...,
1,..., t)
t) n = 1
n = 1  F,
F,  1pi
1pi  F(
F( ),
), = ai+1
= ai+1  Fi = F(
Fi = F( ,
, 1,...,
1,..., i)
i) F[X]
F[X] A3
A3 {1}
{1}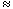 Z2,
Z2,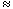 Z3. Thus, S3 is solvable. A composition series for S4 is given by
Z3. Thus, S3 is solvable. A composition series for S4 is given by A4
A4 {(1),(12)(34),(13)(24),(14)(23)}
{(1),(12)(34),(13)(24),(14)(23)} {(1),(12)(34)}
{(1),(12)(34)} {1}.
{1}.