|
The Galois Group of a Polynomial
In the introduction we promised that we would associate to a polynomial a finite group which reflects the algebraic properties of the polynomial. We have now reached the point where that promise is very simple to fulfill.
Let F be a field and let
f = X n + a 1X n-1 + ... + a n  F[X]
be a nonconstant polynomial. Let us fix an algebraic closure F of F. Then, in F[X], we can write
f =  (X -  i i)
where  1,..., 1,..., n are the zeros of f in F. By Theorem 1 of the section on the restrictive assumption, n are the zeros of f in F. By Theorem 1 of the section on the restrictive assumption,  1,..., 1,..., n are all distinct. The splitting field Ef of f over F is given by n are all distinct. The splitting field Ef of f over F is given by
E f = F(  1 1,...,  n n).
It is clear that Ef is a normal extension of F and is therefore a Galois extension of degree m, say.
Definition 1: The Galois group of f over F denoted GalF(f ), is the finite group Gal(Ef /F).
By Theorem 4 of the section on Galois group of an extension, we have
Proposition 2: The order of GalF(f ) is m.
A typical element  of GalF(f ) is an F-automorphism of Ef. But since Ef is generated over F by of GalF(f ) is an F-automorphism of Ef. But since Ef is generated over F by  1,..., 1,..., n, n,  is completely determined once is completely determined once  ( ( i) (i = 1,...,n) is specified. Let us try to pin down what i) (i = 1,...,n) is specified. Let us try to pin down what  ( ( i) can be. i) can be.
Lemma 3: (1) The image of  i is an i is an  j for some j depending on i. In other words j for some j depending on i. In other words  ( ( i) = i) =  j(i) for some j(i) (1 < j(i) < n), j(i) for some j(i) (1 < j(i) < n),
(2) If  j(i) = j(i) =  j(i'), then i = i'. j(i'), then i = i'.
Proof: (1) Clearly  ( ( i) equals some F-conjugate of i) equals some F-conjugate of  i, so that i, so that  ( ( i) is a zero of IrrF( i) is a zero of IrrF( i,X) (by Proposition 2 of the section on conjugates). But since f i,X) (by Proposition 2 of the section on conjugates). But since f  F[X] has F[X] has  i as a zero, IrrF( i as a zero, IrrF( i,X)|f. Therefore, i,X)|f. Therefore,  ( ( i) is a zero of f and i) is a zero of f and  ( ( i) = i) =  j(i) for some j(i) (1 < j(i) < n). j(i) for some j(i) (1 < j(i) < n).
(2) If  j(i) = j(i) =  j(i'), then j(i'), then  ( ( i) = i) =  ( ( i'), But since i'), But since  is an injection, this implies that is an injection, this implies that  i = i =  i'. Therefore, i = i', since all i'. Therefore, i = i', since all  i are distinct. i are distinct.
Lemma 3 asserts that the set { ( ( 1),..., 1),..., ( ( n)} coincides with the set { n)} coincides with the set { 1,..., 1,..., n}. For, indeed { n}. For, indeed { ( ( 1),..., 1),..., ( ( n)} n)}  { { 1,..., 1,..., n} by (1); and { n} by (1); and { ( ( 1),..., 1),..., ( ( n)} contains n distinct elements by (2). In other words, n)} contains n distinct elements by (2). In other words,
P  = 
is a permutation of the n distinct zeros { 1,..., 1,..., n}. It is trivial to verify that the mapping n}. It is trivial to verify that the mapping
 : Gal F( f )  S n,
(1)
is a homomorphism. Moreover, since  is completely determined by
is completely determined by  ( ( 1),..., 1),..., ( ( n), we see that n), we see that  is an injection. Therefore, we have proved: is an injection. Therefore, we have proved:
Theorem 4: GalF(f ) is isomorphic to a subgroup of the group of permutations of the zeros  1,..., 1,..., n. n.
Corollary 5: GalF(f ) is isomorphic to a subgroup of Sn.
Corollary 6: GalF(f ) has order of at most n!
Note that the isomorphism  of (1) will not generally be surjective, so that GalF (f ) will not generally contain all the permutations on of (1) will not generally be surjective, so that GalF (f ) will not generally contain all the permutations on  1,..., 1,..., n. The reader is referred to the examples below for instances of this phenomenon. In Examples 1-4, let F = Q n. The reader is referred to the examples below for instances of this phenomenon. In Examples 1-4, let F = Q
Example 1: f = X2 - 2. Then Ef = Q( and GalF(f ) consists of the mappings and GalF(f ) consists of the mappings
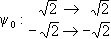 , 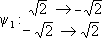 .
Thus, GalF(f ) 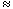 Z2. Z2.
Example 2: f = (X2 - 2)(X2 - 3). Here Ef = Q( , ,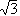 ) and ) and  1 = 1 =  , ,  2 = - 2 = -  , ,  3 = 3 = 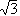 , ,  4 = - 4 = - 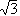 ,
Then GalF(f ) consists of the mappings ,
Then GalF(f ) consists of the mappings
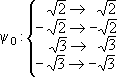 , 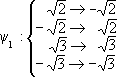 ,
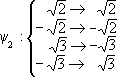 , 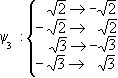 .
Moreover, G1 = { 0, 0, 1} and G2 = { 1} and G2 = { 0, 0, 2} are subgroups of GalF(f ) isomorphic to Z2 and 2} are subgroups of GalF(f ) isomorphic to Z2 and
Example 3: f = X3 - 2. Then  1 = 1 =  , ,  2 = 2 =  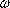 , ,  3 = 3 =  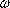 2, where 2, where  denotes a real cube root of 2 and denotes a real cube root of 2 and 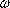 is a primitive cube root of unity. Let us show that GalQ( f ) is a primitive cube root of unity. Let us show that GalQ( f ) 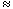 S3, so that all permutations of the roots S3, so that all permutations of the roots  1, 1,  2, 2,  3 correspond to a Galois group. By Theorem 4,
GalQ( f ) is isomorphic to a subgroup of S3. Moreover, Ef/Q is a Galois extension, so that by Theorem 4 of the section the Galois group of an extension, the order of GalQ( f ) equals deg(Ef /Q). Therefore, it suffices to show that deg(Ef /Q) > 6. and this was proved in Example 3 of the section of examples of splitting fields. 3 correspond to a Galois group. By Theorem 4,
GalQ( f ) is isomorphic to a subgroup of S3. Moreover, Ef/Q is a Galois extension, so that by Theorem 4 of the section the Galois group of an extension, the order of GalQ( f ) equals deg(Ef /Q). Therefore, it suffices to show that deg(Ef /Q) > 6. and this was proved in Example 3 of the section of examples of splitting fields.
Example 4: Let f = X5 - 6X + 3. We will show that GalQ( f ) 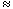 S5. Let us begin by considering the function f(x) = x5 - 6x + 3 for real x. From elementary calculus, we see that this function has a maximum for x = -(6/5)1/4 and a minimum at (6/5)1/4. Moreover, these are the only extrema of f(x). Thus, we may sketch the graph of f(x) as in figure 1, and wee see immediately that f has exactly three real zeros, S5. Let us begin by considering the function f(x) = x5 - 6x + 3 for real x. From elementary calculus, we see that this function has a maximum for x = -(6/5)1/4 and a minimum at (6/5)1/4. Moreover, these are the only extrema of f(x). Thus, we may sketch the graph of f(x) as in figure 1, and wee see immediately that f has exactly three real zeros,  3, 3,  4, and 4, and  5. Let 5. Let  1 = a + b 1 = a + b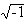  C be a nonreal zero of f. C be a nonreal zero of f.
Figure 1: Graph of f(x) = x5 - 6x + 3.
If  = x + y = x + y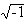 (x,y (x,y  R) is a complex number, let us define the complex conjugate of R) is a complex number, let us define the complex conjugate of 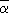 of of  by by
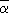 = x - y 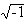 .
The mapping   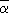 is an automorphism of C. From this fact it follows that is an automorphism of C. From this fact it follows that
0 = 0 = 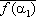
= 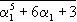
= 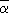 15 15 - 6 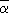 1 1 +3
= f( 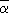 1 1).
Therefore,  2 = 2 = 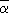 1 is a zero of f and Ef = Q( 1 is a zero of f and Ef = Q( 1, 1, 2, 2, 3, 3, 4, 4, 5). 5).
The mapping  : Ef : Ef Ef defined by Ef defined by  ( ( ) = ) = 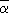 is a Q-automorphism of Ef and therefore is a Q-automorphism of Ef and therefore   GalQ( f ). Moreover, GalQ( f ). Moreover,
Therefore, when  is viewed as a permutation, is viewed as a permutation,  is just the permutation (12), which interchanges is just the permutation (12), which interchanges  1 and 1 and  2 and leaves all other 2 and leaves all other  i fixed. Therefore, we have located one specific element of GalQ( f ). i fixed. Therefore, we have located one specific element of GalQ( f ).
By the Eisenstein irreducibility criterion, f is irreducible in Q[X], so that deg(Q( 1)/Q) = 5 by Theorem 3 of the section on algebraic numbers. Therefore, since 1)/Q) = 5 by Theorem 3 of the section on algebraic numbers. Therefore, since
deg(E f / Q) = deg(E f / Q(  1 1))·deg( Q(  1 1)/ Q),
we see that deg(Ef /Q) is divisible by 5. Therefore, by Proposition 2 and Theorem 4, GalQ( f ) is a subgroup of the group of permutations of  1,... 1,... 5 and that the order of GalQ( f ) is divisible by 5. Moreover, by the first Sylow Theorem, GalQ( f ) contains a subgroup H of order 5. In particular, GalQ( f ) contains an element 5 and that the order of GalQ( f ) is divisible by 5. Moreover, by the first Sylow Theorem, GalQ( f ) contains a subgroup H of order 5. In particular, GalQ( f ) contains an element  of order 5. Let of order 5. Let
 = (i 1...i r)(j 1...j s)(k 1...k t)...
be the decomposition of  into a product of disjoint cycles. The order of into a product of disjoint cycles. The order of  is the least common multiple of r,s,t, ..., Therefore, since is the least common multiple of r,s,t, ..., Therefore, since  has order 5, has order 5,  must be a 5-cycle, say must be a 5-cycle, say
 = (1i 2i 3i 4i 5).
By replacing  by some power of by some power of  , we may assume , we may assume  has the form has the form
 = (12i 3i 4i 5).
However, by permuting and renumbering the  3, 3, 4, 4, 5, we may assume that 5, we may assume that
 = (12345).
Therefore, we have shown that GalQ( f ) contains the permutations (12), (12345). However, it is easy to check that for r = 0,1,2,3,
(12345)-r(12)(12345)r = (r + 1, r + 2),
(12345)-4(12)(12345)4 = (51).
Therefore, GalQ( f ) contains the transpositions (12), (23), (34), (45), and (51). And these transpositions generate all transpositions. Therefore, since S5 is generated by transpositions, GalQ( f ) = S5.
Example 5: Let  be a primitive mth root of 1 and let F be a field containing be a primitive mth root of 1 and let F be a field containing  . Let a . Let a  F, f = Xm - a F, f = Xm - a  F[X], and let E = the splitting field of f over F. If b is a zero of f in F, then the zeros of f ar given by F[X], and let E = the splitting field of f over F. If b is a zero of f in F, then the zeros of f ar given by
b,b  ,...,b  m-1 m-1,
so that f = (X - b)...(X - b m-1) in F[X], and E = F(b) since m-1) in F[X], and E = F(b) since   F. If F. If   GalF( f ), then there exists a unique integer a( GalF( f ), then there exists a unique integer a( ) such that ) such that
 (b) = b  a( a( ) ), 0 < a(  ) < m - 1.
Let  : GalF( f ) : GalF( f )  Zm be defined by Zm be defined by
Then  is an injection. Moreover, is an injection. Moreover,
=  (b) ·  a( a( ) ) (since   F and  is an F-automorphism of E)
On the other hand, (  )(b) = b )(b) = b a( a( )+b( )+b( ), so that ), so that  a( a( )+b( )+b( )-a( )-a(  ) = 1 and a( ) = 1 and a( ) +b( ) +b( ) - a( ) - a(  ) )  0 (mod m). Thus, 0 (mod m). Thus,
and  is an isomorphism. We have proved that GalF( f ) is isomorphic to a subgroup of Zm. In particular, since Zm is a cyclic group, GalF( f ) is cyclic. It is not usually true that GalF( f ) is an isomorphism. We have proved that GalF( f ) is isomorphic to a subgroup of Zm. In particular, since Zm is a cyclic group, GalF( f ) is cyclic. It is not usually true that GalF( f ) 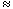 Zm. Zm.
|
 1,...,
1,..., n.
n.
 1,...,
1,..., n.
The order of
n.
The order of  be algebraic over F,
be algebraic over F,  ,X)).
,X)). )/F) = n.
)/F) = n.
 ,
, 2,...,
2,..., n-1} is a basis for F(
n-1} is a basis for F( ) over F.
Let
) over F.
Let  Z[X]
Z[X] an,
an, a0.
a0.
 F.
F. is algebraic over F. Let
is algebraic over F. Let  ,X).
,X). 1)(X -
1)(X -  2)...(X -
2)...(X -  n),
n),  i
i  F,
F,  1 =
1 =  .
. 1,...,
1,..., n are called the conjugates of
n are called the conjugates of  over F.
The set of real numbers.
The complex numbers.
The set residue classes mod n.
The set of rational numbers.
A function
over F.
The set of real numbers.
The complex numbers.
The set residue classes mod n.
The set of rational numbers.
A function  B
B B
B A
A
 E
E ).
). be an F-isomorphism of E into F. Then
be an F-isomorphism of E into F. Then  has the form (1), where
has the form (1), where  (
( )
) over F. In particular, there are at most n F-isomorphisms of E into F.
Let
over F. In particular, there are at most n F-isomorphisms of E into F.
Let 
 E be algebraic over F.
E be algebraic over F.  the zero of a monic irreducible polynomial
the zero of a monic irreducible polynomial  F[X]
F[X] over F denoted
over F denoted  ,X)
,X) B
B
 E
E ).
). 1,...,
1,..., n be the conjugates of
n be the conjugates of  over F and let
over F and let  i
i  G(E/F)
G(E/F) i(
i( ) =
) =  i.
i. i
i  Gal(E/F)
Gal(E/F) i
i  E.
E. i belong to E and
i belong to E and  F[X].
F[X].
 1,...,
1,..., n)
n) F[X]
F[X] F[X]
F[X] (X -
(X -  i)
i) 1,...,
1,..., n).
n). =
= 
 : GalF(f )
: GalF(f )  Sn,
Sn, (
( ) = P
) = P
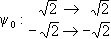 ,
, 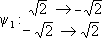 .
.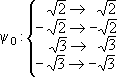 ,
, 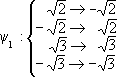 ,
,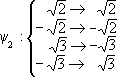 ,
, 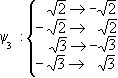 .
.
 = x - y
= x - y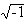 .
.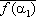
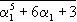
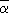 15 - 6
15 - 6  1 +3
1 +3 1).
1). (
( 1) =
1) =  2,
2, (
( 2) =
2) =  1,
1, (
( i) =
i) =  i, (i = 3,4,5)
i, (i = 3,4,5) = (i1...ir)(j1...js)(k1...kt)...
= (i1...ir)(j1...js)(k1...kt)... = (1i2i3i4i5).
= (1i2i3i4i5). = (12i3i4i5).
= (12i3i4i5). = (12345).
= (12345). ,...,b
,...,b m-1,
m-1, (b) = b
(b) = b a(
a( ), 0 < a(
), 0 < a( ) < m - 1.
) < m - 1. (
( ) = a(
) = a( ) (mod m).
) (mod m).
 )(b) =
)(b) =  (b
(b a(
a( ))
)) (b) ·
(b) ·  a(
a( ) (since
) (since 
 F and
F and  is an F-automorphism of E)
is an F-automorphism of E) a(
a( )+b(
)+b( ).
). (
(
 ) =
) =  (
( ) +
) +  (
( ),
),