Let E be an extension of F of degree n, and let 
 E be such that E = F(
E be such that E = F( ). Further, let
). Further, let  1,...,
1,..., n be the conjugates of
n be the conjugates of  over F. Then
over F. Then
(1)  1,...,
1,..., n are distinct.
n are distinct.
(2) For each i (1 < i < n), the exists an F-isomorphism  of E into F such that
of E into F such that  i(
i( ) =
) =  i. Moreover,
i. Moreover,  i is unique and is given by
i is unique and is given by
 i(b0 + b1
i(b0 + b1 + ... + bn-1
+ ... + bn-1 n-1) = b0 + b1
n-1) = b0 + b1 i + ... + bn-1
i + ... + bn-1 in-1, bj
in-1, bj  F.
F.
(3) There are exactly n F-isomorphisms of E into F and these are  1,...,
1,..., n.
n.
|
The Galois Group of an Extension
Let F be a field and let E be a finite extension of F. Our objective at this point is to associate a finite group to the extension E/F, called the Galois group. We will show how it is possible to utilize the Galois group to describe the arithmetic of the extension. In this section we will limit ourselves to defining the Galois group and computing some examples.
Definition 1: An F-automorphism of E is an F-isomorphism of E onto itself. The set of all F-automorphisms of E will be denoted Gal(E/F).
Since an F-automorphism of E is an F-isomorphism of E into F, we see that Gal(E/F)  G(E/F). Therefore, Theorem 4 of the section on conjugates implies the following result. G(E/F). Therefore, Theorem 4 of the section on conjugates implies the following result.
Lemma 2: Suppose that deg(E/F) = n. Then Gal(E/F) contains at most n elements.
The following lemma helps to pick out the elements of Gal(E/F) from G(E/F).
Lemma 3: Let   G(E/F). Then G(E/F). Then   Gal(E/F) if and only if Gal(E/F) if and only if  (E) (E)  E. E.
Proof:  Obvious. Obvious.
 It suffices to show that if It suffices to show that if  (E) (E)  E, then E, then  (E) = E. Suppose the deg(E/F) = n, and let { (E) = E. Suppose the deg(E/F) = n, and let { 1,..., 1,..., n} be a basis of E over F. Since n} be a basis of E over F. Since  is an F-isomorphism, { is an F-isomorphism, { ( ( 1),..., 1),..., ( ( n)} is a basis of n)} is a basis of  (E) over F. Thus, deg( (E) over F. Thus, deg( (E)/F) = n. However, since (E)/F) = n. However, since  (E) (E)  E, E,
deg(E/F) = deg(  (E)/F) · deg(E/  (E)),
and thus deg(E/ (E)) = 1, which implies that E = (E)) = 1, which implies that E =  (E). (E).
By Lemma 3 and Theorem 4 of the section on conjugates, we can deduce the following description of Gal(E/F):
Theorem 4: Let E be an extension of F of degree n, and let   E be such that E = F( E be such that E = F( ). Further, let ). Further, let  1,..., 1,..., n be the conjugates of n be the conjugates of  over F and let over F and let  i i  G(E/F) be such that G(E/F) be such that  i( i( ) = ) =  i. Then i. Then  i i  Gal(E/F) if and only if Gal(E/F) if and only if  i i  E. In particular, if E is a normal extension of F, then all E. In particular, if E is a normal extension of F, then all  i belong to E and Gal(E/F) contains n elements. i belong to E and Gal(E/F) contains n elements.
Let us define a group structure on Gal(E/F). If  , ,  Gal(E/F). the the composite function Gal(E/F). the the composite function   , defined by , defined by
is an F-automorphism of E. Indeed,   is a homomorphism of E into E such that ( is a homomorphism of E into E such that (  )(1) = 1. Therefore, )(1) = 1. Therefore,   is an isomorphism by Proposition 2 of the introduction to field theory. And since is an isomorphism by Proposition 2 of the introduction to field theory. And since  and and  are F-isomorphisms, if x are F-isomorphisms, if x  F, we have ( F, we have (  )(x) = )(x) =  ( ( (x)) = (x)) =  (x) = x. Therefore, (x) = x. Therefore,   is an F-isomorphism of E into E, so that by Lemma 3, is an F-isomorphism of E into E, so that by Lemma 3,   is an F-automorphism of E. Let us define the product of is an F-automorphism of E. Let us define the product of  and and  to be the F-automorphism to be the F-automorphism   . With respect to this law of multiplication, Gal(E/F) is a group. Indeed, the identity automorphism i defined i(x) = x for all x . With respect to this law of multiplication, Gal(E/F) is a group. Indeed, the identity automorphism i defined i(x) = x for all x  E. If E. If   Gal(E/F), let Gal(E/F), let  -1 denote the inverse function of -1 denote the inverse function of  , when , when  is considered as a bijection from E onto E. Then is considered as a bijection from E onto E. Then  -1 is an F-automorphism of E, and -1 is an F-automorphism of E, and   -1 = -1 =  -1 -1 = i. = i.
Definition 5: Gal(E/F) is called the Galois group of the extension E over F.
Let us compute Gal(E/F) in a few examples.
Example 1: F = Q, E = Q( ). Then E is a normal extension of F and Gal(E/F) = { ). Then E is a normal extension of F and Gal(E/F) = { 0, 0,  1}, where 1}, where
The mapping  :Gal(E/F) :Gal(E/F) Z2 defined by Z2 defined by  ( ( a) = a (mod 2) is a surjective isomorphism. Therefore, Gal(E/F) a) = a (mod 2) is a surjective isomorphism. Therefore, Gal(E/F)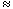 Z2. Z2.
Example 2: F = Q, E = Q( m), where m), where  m is a primitive mth root of 1. Then E is a normal extension of F of degree m is a primitive mth root of 1. Then E is a normal extension of F of degree  (n). The conjugates of (n). The conjugates of  m are m are  ma (0 < a < m - 1, (a,m) = 1). Therefore, Gal(E/F) has order ma (0 < a < m - 1, (a,m) = 1). Therefore, Gal(E/F) has order  (n) and consists of the elements (n) and consists of the elements  a (0 < a < m -1, (a,m) = 1) defined by a (0 < a < m -1, (a,m) = 1) defined by
Notice that
 a a b b(  m m) =  a a(  mb mb) =  a a(  m m) b =  mab mab.
Therefore, if q and c are integers such that ab = qm + c, 0 < c < m - 1, we have
(1)
 a a b b(  m m) =  mqm+c mqm+c = (  mm mm) q  mc mc =  c c(  m m)
since  mm = 1. Let mm = 1. Let  :Gal(E/F) :Gal(E/F) Zmx be the mapping defined by Zmx be the mapping defined by  ( ( a) = a (mod m). Then formula (1) implies that a) = a (mod m). Then formula (1) implies that
 (  a a b b) = c(mod m) = ab(mod m) =  (  a a)  (  b b).
Therefore,  is a homomorphism. It is clear that is a homomorphism. It is clear that  is a bijection, and thus is a bijection, and thus
Gal(E/F) 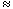 Zmx Zmx. Example 3: F = Q, E = Q( ), where ), where  denotes the real cube root of 2. The conjugates of denotes the real cube root of 2. The conjugates of  over Q are over Q are  , ,  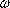 , ,  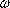 2, where 2, where 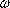 = (-1 + = (-1 + 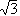 i)/2. The only conjugate of i)/2. The only conjugate of  which lies in E is which lies in E is  , so that , so that
Gal(E/F) = {  0 0},
where  0( 0( ) = ) =  . Note that deg(E/F) = 3, but the order of Gal(E/F) is 1. This is not a contradiction to our above discussion since E is not a normal extension of F. . Note that deg(E/F) = 3, but the order of Gal(E/F) is 1. This is not a contradiction to our above discussion since E is not a normal extension of F.
|

 G(E/F).
G(E/F).
 Gal(E/F)
Gal(E/F) (E)
(E)  E.
E.
 G(E/F).
G(E/F).
 Gal(E/F)
Gal(E/F) (E)
(E)  E.
E. F[X].
F[X].
 E
E ).
). 1,...,
1,..., n be the conjugates of
n be the conjugates of  over F. Then
over F. Then
 1,...,
1,..., n are distinct.
n are distinct. of E into F such that
of E into F such that  i(
i( ) =
) =  i. Moreover,
i. Moreover,  i is unique and is given by
i is unique and is given by
 i(b0 + b1
i(b0 + b1 + ... + bn-1
+ ... + bn-1 n-1)
n-1) i + ... + bn-1
i + ... + bn-1 in-1, bj
in-1, bj  F.
F. 1,...,
1,..., n.
n.
 (E)/F) · deg(E/
(E)/F) · deg(E/ (E)),
(E)),
 )(x) =
)(x) =  (
( (x))
(x))