 F[X]
F[X] F[X]
F[X]| Back | Table of Contents |
|
|
The Fundamental Theorem of Galois TheoryLet us now determine what information about an extension E of F can be gleaned from the Galois group. Usually, very little can be said. For example, Example 3 of the section on Galois groups, shows that E can be of degree > 1, while the Galois group is of order 1. In this case one would not expect the Galois group to contain very much information about the extension. In some sense, the Galois group is "too small." However, we have shown that if E is a normal extension of F, then the order of Definition 1: If E is a normal extension of F, then we say that E/F is a Galois extension. Let us fix a Galois extension E/F of degree n and let
F
 D D  E. E.The fundamental theorem of Galois theory allows a complete description of all intermediate fields D in terms of the Galois group G. One way of manufacturing an intermediate field is as follows: Let H be a subgroup of G, and set (1) (H) = {x (H) = {x  E | E |  (x) = x for all (x) = x for all   H} H}Then we have
Proposition 2: Proof: It is clear that  (x) = x, (x) = x,  (y) = y for all (y) = y for all   H H  (x ± y) = (x ± y) =  (x) ± (x) ±  (y) = x ± y for all (y) = x ± y for all   H H x ± y x ± y   (H). (H).
Thus,  (x) = x, (x) = x,  (y) = y for all (y) = y for all   H H (xy-1) = (xy-1) =  (x) (x) (y-1) = (y-1) =  (x) (x) (y)-1 (y)-1
= xy-1 for all
  H H xy-1 xy-1   (H). (H).
Therefore, the nonzero elements of We have therefore shown how to go from a subgroup of H of G to an intermediate field
Proposition 3: Let E/F be a Galois extension, H a subgroup of
Gal(E/
 (H)) = H. (H)) = H.Proof: Since E/F is finite and normal, the same is true of
H
 Gal(E/ Gal(E/ (H)). (H)).
Suppose that H has s elements and
s < t.
In order to show that 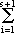  j( j( i)Xi = 0 (1 < j < s). i)Xi = 0 (1 < j < s).
has s equations in s+1 unknowns. By Theorem 6 of the section on linear transformations, this system has a solution (c1,...,cs+1),
(c1,c2,...,cr,0,0,...,0), ci
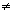 0 (1 < i < r) 0 (1 < i < r)
Since the system (4) is homogeneous, we may normalize cr to be 1 by replacing (5) by the solution (c1cr-1,c2cr-1,...,1,0,0,...,0). If all ci belong to 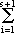  1( 1( i)ci = 0 i)ci = 0  1( 1(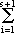  ici) = 0 [since ici) = 0 [since  1 is an 1 is an  (H)-automorphism] (H)-automorphism] 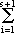  ici = 0, ici = 0,
which is a contradiction to the assumed linear independence of 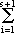   j( j( i) i) (ci) = 0. (ci) = 0.
Therefore, since
(
 (c1), (c1), (c2),..., (c2),..., (cr-1),1,0,0,...,0) (cr-1),1,0,0,...,0)is a solution of the system (4). But the difference of the two solutions of (4) is also a solution of (4), so that we see that
(
 (c1) - c1, (c1) - c1,  (c2) - c2,..., (c2) - c2,..., (cr-1) - cr-1,0,0,...,0) (cr-1) - cr-1,0,0,...,0)
is a solution of (4). Since In our discussion above, we constructed the correspondence
H
  (H), (H),
which associates to a subgroup H of 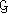 (D) = { (D) = {  G | G |  (x) = x for all x (x) = x for all x  D}. D}.It is clear that (6)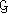 (D) = Gal(E/D). (D) = Gal(E/D).
Therefore, by Proposition 3, if H is any subgroup of 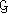 ( ( (H)) = H. (H)) = H.Thus, if D is any intermediate field, (8)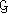 ( ( ( (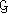 (D))) = (D))) = 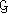 (D) [Equation (7) with H = (D) [Equation (7) with H = 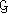 (D)] (D)] deg(E/ deg(E/ ( (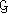 (D))) = | (D))) = |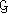 ( ( ( (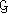 (D)))| (D)))|
[Equation (6) with D replaced by
(9)
 ( (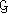 (D)), and Theorem 4 of Galois groups.] (D)), and Theorem 4 of Galois groups.]
= |
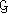 (D)| [Equation (8)] (D)| [Equation (8)]
= deg(E/D)
[Equation (6) and Theorem 4 of Galois groups]
But it is clear that  ( (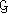 (D)) (D))  D, D,so that by Equation (9),  ( (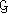 (D))/D) = 1 (D))/D) = 1   ( (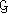 (D)) = D. (D)) = D.Thus, we see that if D is any intermediate field, then (10) ( (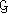 (D)) = D. (D)) = D.
Not that this last equation implies that the intermediate field D is of the form Finally we may state Theorem 4 (Fundamental Theorem of Galois Theory): Let E/F be a Galois extension with Galois group G. Then the correspondence
H
  (H) (H)
is a one-to-one mapping of the set of subgroups G onto the set of intermediate fields for the extension E/F. Moreover, if H corresponds to D under this correspondence, then E/D is a Galois extension and Proof: The face that the correspondence
Corollary 5: Let E/F be a Galois extension. There are only finitely many intermediate fields D such that This result is somewhat surprising. Proof: Example 1: Let 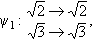 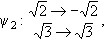 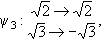 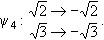
The subgroups of
H1 = {
 1}, H2 = { 1}, H2 = { 1, 1,  2}, H3 = { 2}, H3 = { 1, 1,  3}, 3},
H4 = {
 1, 1,  4}, H5 = { 4}, H5 = { 1, 1, 2, 2,  3, 3,  4}. 4}.The corresponding fixed fields are  (H1) = Q( (H1) = Q( , ,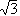 ), ), (H2) = Q( (H2) = Q(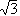 ), ), (H3) = Q( (H3) = Q( ), ), (H4) = Q( (H4) = Q( ), ), (H5) = Q. (H5) = Q.
[The only computation which deserves comment is the one leading to the assertion As a consequence of the fundamental theorem, we see that We shall refer to the correspondence Theorem 6: Let E/F be a Galois extension with Galois group G. Let H1 and H2 be subgroups of G, and let D1 and D2, respectively, correspond to H1 and H2 under Galois correspondence. Then (1) H1 (2) The intermediate field corresponding to (3) The intermediate field corresponding to Proof: By the fundamental theorem
D1 =
 (H1), D2 = (H1), D2 =  (H2). (H2).(1) It is clear that (2) (3) Perhaps the most useful consequence of the fundamental theorem is the following result, which will be used many times throughout this chapter.
Corollary 7: Let E/F be a Galois extension with Galois group G, and let Proof: If
Theorem 8: Let E/F be a Galois extension and let (1) D/F is a normal extension if and only if H is a normal subgroup of G. (2) If H is a normal subgroup of G, then D/F is a Galois extension and Proof: Let 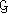 ( ( D) = D) =  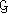 (D) (D) -1. -1.
For if (1)Note that D/F is normal
(2) By part(1), if H is a normal subgroup of G, then D/F is normal. Moreover, it is clear that D/F is finite. Thus D/F is a Galois extension. Let us consider the mapping  :Gal(E/F) :Gal(E/F)  Gal(D/F) Gal(D/F)
which arises by mapping
ker
 = { = {  Gal(E/F) | Gal(E/F) |  = the identity on D} = the identity on D}
= H.
Therefore, by the first isomorphism theorem,
G/H
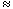 Gal(D/F). Gal(D/F). |
| Back | Table of Contents |