|
Conjugates and Normal Extensions
Let F be a field, F its algebraic closure,   F. Then F. Then  is algebraic over F. Let f = IrrF( is algebraic over F. Let f = IrrF( ,X). Then ,X). Then
f = (X -  1 1)(X -  2 2)...(X -  n n),  i i  F F,  1 1 =  .
Definition 1: The elements  1,..., 1,..., n are called the conjugates of n are called the conjugates of  over F. over F.
Example 1: If   F, then IrrF( F, then IrrF( ,X) = X - ,X) = X -  and the only conjugate of and the only conjugate of  over F is over F is  itself. itself.
Example 2: Let F = Q,  = = 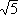 . Then IrrQ( . Then IrrQ( ,X) = X2 - 5, and the conjugates of ,X) = X2 - 5, and the conjugates of  over Q are over Q are 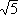 and - and -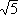 . .
Example 3: Let F = Q,  = (-1 + = (-1 + 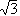 i)/2. Then IrrQ( i)/2. Then IrrQ( ,X) = X2 + X + 1, so that the conjugates of ,X) = X2 + X + 1, so that the conjugates of  over Q are (-1 + over Q are (-1 + 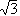 i)/2, (-1 - i)/2, (-1 - 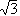 i)/2. i)/2.
Example 4: Let F = Q,  = =  , a primitive nth root of 1. Then IrrQ( , a primitive nth root of 1. Then IrrQ( ,X) = ,X) =  n(X), the nth cyclotomic polynomial. Therefore, the conjugates of n(X), the nth cyclotomic polynomial. Therefore, the conjugates of  over Q are over Q are  a [0 < a < n - 1, (a,n) = 1]. a [0 < a < n - 1, (a,n) = 1].
Example 5: Let F = Q,  = =  . Then IrrQ( . Then IrrQ( ,X) = X3 - 2. Therefore, the conjugates of ,X) = X3 - 2. Therefore, the conjugates of  over Q are over Q are  , ,  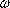 , ,  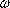 2, where 2, where 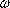 = (-1 + = (-1 + 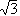 i)/2 is a primitive cube root of 1. i)/2 is a primitive cube root of 1.
Let E be a finite extension of F. Let us use the notion of conjugate elements to determine all the F-isomorphisms of E into F. Since E is a finite extension of F, E is an algebraic extension of F and there exist  1,..., 1,..., n n  E such that E = F( E such that E = F( 1,..., 1,..., n). By Corollary 4 of our restrictive assumption, there exists n). By Corollary 4 of our restrictive assumption, there exists   E such that E = F( E such that E = F( ). Moreover, by Theorem 3 of the section on algebraic numbers, every element x of E can be written uniquely in the form ). Moreover, by Theorem 3 of the section on algebraic numbers, every element x of E can be written uniquely in the form
x = a 0 + a 1 + ... + a n-1 n-1 n-1, a i  F, n = deg(E/F).
Therefore, if  is an F-isomorphism of E into F, then is an F-isomorphism of E into F, then
(1)
 (x) =  (a 0) +  (a 1)  (  ) + ... +  (a n-1)  (  ) n-1
= a 0 + a 1 (  ) + ... + a n-1 (  ) n-1.
Thus,  is completely determined once is completely determined once  ( ( ) is specified. We assert that ) is specified. We assert that  ( ( ) is a conjugate of ) is a conjugate of  over F. Let f = b0 + b1X + ... + bn-1Xn-1 + Xn = IrrF( over F. Let f = b0 + b1X + ... + bn-1Xn-1 + Xn = IrrF( ,X) Then ,X) Then
0 = b 0 + b 1 + ... + b n-1 n-1 n-1 +  n n
 0 =  (0) =  (b 0 + b 1 + ... + b n-1 n-1 n-1 +  n n)
=  (b 0) +  (b 1)  (  ) + ... +  (b n-1)  (  ) n-1 +  (  ) n
= b 0 + b 1 (  ) + ... + b n-1 (  ) n-1 +  (  ) n
= f(  (  )).
Therefore,  ( ( ) is a zero of f, and hence is a conjugate of ) is a zero of f, and hence is a conjugate of  over F. We may summarize our findings in the following proposition. over F. We may summarize our findings in the following proposition.
Proposition 2: Let E be an extension of F of degree n and let   E be such that E = F( E be such that E = F( ). Further, let ). Further, let  be an F-isomorphism of E into F. Then be an F-isomorphism of E into F. Then  has the form (1), where has the form (1), where  ( ( ) is a conjugate of ) is a conjugate of  over F. In particular, there are at most n F-isomorphisms of E into F. over F. In particular, there are at most n F-isomorphisms of E into F.
We will refine Proposition 2 by determining precisely all the F-isomorphisms of E into F. As a first step in this direction, let us establish the following general result.
Theorem 3: Let F be a field, F( ) an algebraic extension of F of degree n, K an algebraically closed field, f = IrrF( ) an algebraic extension of F of degree n, K an algebraically closed field, f = IrrF( ,X). Suppose that an isomorphism ,X). Suppose that an isomorphism  : F : F K is given. If K is given. If
f = a 0 + a 1X + ... + a n-1X n-1 + X n  F[X],
let us define
f  =  (a 0) +  (a 1)X + ... +  (a n-1)X n-1 + X n  K[X],
Let  be any zero of f be any zero of f  in K. Then there exists an isomorphism in K. Then there exists an isomorphism  : F( : F( ) )  K such that (1) the restriction of K such that (1) the restriction of  to F coincides with to F coincides with  and (2) and (2)  ( ( ) = ) =  . In other words, . In other words,  is an extension of is an extension of  to F( to F( ) which maps ) which maps  to to  . .
Proof: Every element x of F( ) can be uniquely written in the form ) can be uniquely written in the form
(2)
x = a 0 + a 1 + ... + a n-1 n-1 n-1, a i F.
Therefore, let us define  :F( :F( ) ) K by K by
(3)
 (x) =  (a 0) +  (a 1)  + ... +  (a n-1)  n-1 n-1.
It is clear that  restricted to F equals restricted to F equals  and that and that  ( ( ) = ) =  . Thus, it remains to prove that . Thus, it remains to prove that  is an isomorphism. Let x be defined by (2) and let is an isomorphism. Let x be defined by (2) and let
y = b 1 + b 1 + ... + b n-1 n-1 n-1, b i  F.
It is straightforward to verify that  (x + y) = (x + y) =  (x) + (x) +  (y). Let us show that (y). Let us show that  (x · y) = (x · y) =  (x) · (x) ·  (y). Set g = (y). Set g = 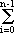 aiXi, h = aiXi, h =  bjXj. By the division algorithm in F[X]. there exist polynomials q,r bjXj. By the division algorithm in F[X]. there exist polynomials q,r  F[X] such that F[X] such that
(4)
g · h = q · f + r, r = do + d1X + .. + dn-1Xn-1
Since f( ) = 0, (4) implies that ) = 0, (4) implies that
Fo any polynomial k = e0 + e1X + .. + esXs  F[X]. set F[X]. set
k  =  (e 0) +  (e 1)X + ... +  (e s)X s  K[X],
Then by the definitions of  and the fact that f and the fact that f  ( ( ) = 0, we have ) = 0, we have
=( f · q + r)  (  )
= (g · h)  (  )
=  (x) ·  (y).
Thus,  is a homomorphism. But since is a homomorphism. But since  (1) = 1 (1) = 1 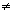 0, Proposition 2 in the introduction to the theory of fields implies that 0, Proposition 2 in the introduction to the theory of fields implies that  is an isomorphism. is an isomorphism.
It is now easy to determine all F-isomorphisms of E into F.
Theorem 4: Let E be an extension of F of degree n, and let   E be such that E = F( E be such that E = F( ). Further, let ). Further, let  1,..., 1,..., n be the conjugates of n be the conjugates of  over F. Then over F. Then
(1)  1,..., 1,..., n are distinct. n are distinct.
(2) For each i (1 < i < n), the exists an F-isomorphism  of E into F such that of E into F such that  i( i( ) = ) =  i. Moreover, i. Moreover,  i is unique and is given by i is unique and is given by
(5)
 i i(b 0 + b 1 + ... + b n-1 n-1 n-1)
= b 0 + b 1 i i + ... + b n-1 in-1 in-1, b j  F. (3) There are exactly n F-isomorphisms of E into F and these are  1,..., 1,..., n. n.
Proof: (1)  1,..., 1,..., n are the zeros of Irrf( n are the zeros of Irrf( ,X), Therefore, ,X), Therefore,  1,..., 1,..., n are distinct by Theorem 1 of the restrictive assumption. n are distinct by Theorem 1 of the restrictive assumption.
(2) Let  :F :F F be the isomorphism defined by F be the isomorphism defined by  (x) = x (x (x) = x (x  F). Then f F). Then f  = f and Theorem 3 implies that there exists an F-isomorphism = f and Theorem 3 implies that there exists an F-isomorphism  i such that i such that  i( i( ) = ) =  i. Moreover, by (1), i. Moreover, by (1),  1 is given by (5). 1 is given by (5).
(3) By Proposition 2, the number of F-isomorphisms of E into F is at most n. Since the  i are all distinct by part (1), the i are all distinct by part (1), the  i are all distinct. Therefore, we have exhibited n different F-isomorphisms of E into F. This proves part (3). i are all distinct. Therefore, we have exhibited n different F-isomorphisms of E into F. This proves part (3).
The isomorphisms  i (1 < i < n) are called conjugation mappings for the extension E of F. Let us denote the set of all conjugation mappings by G(E/F). For example, if F = Q, E = Q( i (1 < i < n) are called conjugation mappings for the extension E of F. Let us denote the set of all conjugation mappings by G(E/F). For example, if F = Q, E = Q( ), then ), then
G(E/F) = {  1 1,  2 2},
where  1( 1( ) = ) =  and and  2( 2( ) = - ) = - . If F = Q, E = Q( . If F = Q, E = Q( ), then ), then
where 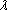 1( 1( ) = ) =  , , 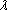 2( 2( ) = ) =  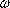 , , 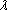 3( 3( ) = ) =  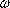 2. 2.
Note that the extension F( ) may not contain all the conjugates of ) may not contain all the conjugates of  . For example, Q( . For example, Q( ) )  R, but R, but  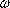 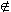 R. The extensions which are obtained by adjoining to F all of the conjugates of a set of elements of F are a very important class of extensions, called normal extensions. More precisely, let us make the following definition. R. The extensions which are obtained by adjoining to F all of the conjugates of a set of elements of F are a very important class of extensions, called normal extensions. More precisely, let us make the following definition.
Definition 5: Let F be a field. A normal extension of F is an extension of F obtained by adjoining all zeros of a finite set of polynomials {f1,...,fm}, fj  F[X]. F[X].
For example, if f  F[X] is a nonconstant polynomial, then the splitting field Ef of f is a normal extension of F. Since a normal extension of F is gotten by adjoining a finite number of algebraic elements to F, a normal extension is finite and algebraic. Let us derive a number of equivalent conditions for an extension of F to be normal. F[X] is a nonconstant polynomial, then the splitting field Ef of f is a normal extension of F. Since a normal extension of F is gotten by adjoining a finite number of algebraic elements to F, a normal extension is finite and algebraic. Let us derive a number of equivalent conditions for an extension of F to be normal.
Theorem 6: Let F be a field, E a finite algebraic extension of F. The the following conditions are equivalent:
(1) E is the splitting field of a polynomial f  F[X]. F[X].
(2) E is a normal extension of F.
(3) If   G(E/F), then G(E/F), then  (E) = E. (E) = E.
(4) If x  E, then all conjugates of x over F lie in E. E, then all conjugates of x over F lie in E.
Proof: We will prove the theorem by proving the series of implications
(1) (2) (2) (3) (3) (4) (4) (1). (1).
(1) (2). We observed this fact above. (2). We observed this fact above.
(2) (3). Suppose that E is a normal extension of F and that (3). Suppose that E is a normal extension of F and that   G(E/F). Then E is obtained from F by adjoining all zeros { G(E/F). Then E is obtained from F by adjoining all zeros { 1,..., 1,..., s} of a finite collection of polynomials {f1,...,fm}, fj s} of a finite collection of polynomials {f1,...,fm}, fj  F[X]. In particular, if F[X]. In particular, if   { { 1,..., 1,..., s}, then all conjugates of s}, then all conjugates of  over F belong to { over F belong to { 1,..., 1,..., s}, and hence to E = F( s}, and hence to E = F( 1,..., 1,..., s). But s). But  ( ( i) is one of the conjugates of i) is one of the conjugates of  i over F. Therefore, i over F. Therefore,  ( ( i) i)  E. Hence, since E. Hence, since  is an F-isomorphism, we see that is an F-isomorphism, we see that  (E) (E)  E. Let deg(E/F) = n. Then, since E. Let deg(E/F) = n. Then, since  is an F-isomorphism, deg( is an F-isomorphism, deg( (E)/F) = n. Therefore, since F (E)/F) = n. Therefore, since F   (E) (E)  E, and since deg(E/F) = deg(E/ E, and since deg(E/F) = deg(E/ (E)) · deg( (E)) · deg( (E)/F), we see that deg(E/ (E)/F), we see that deg(E/ (E)) = 1. Therefore, E = (E)) = 1. Therefore, E =  (E) by Proposition 2 of the section on algebraic extensions. (E) by Proposition 2 of the section on algebraic extensions.
(3) (4). Suppose the (4). Suppose the   G(E/F) implies that G(E/F) implies that  (E) = E, and assume that x (E) = E, and assume that x  E. Let x' be a conjugate of x over F. We wish to show that x' E. Let x' be a conjugate of x over F. We wish to show that x'  E. By Theorem 3, there exists and F-isomorphism E. By Theorem 3, there exists and F-isomorphism  :F(x) :F(x) F such that F such that  (x) = x'. By
Theorem 3 of the section on the restrictive assumption, there exists (x) = x'. By
Theorem 3 of the section on the restrictive assumption, there exists   E such that E = F(x)( E such that E = F(x)( ). Then, by Theorem 3, ). Then, by Theorem 3,  can be extended to an F-isomorphism can be extended to an F-isomorphism  :E :E F. [Map F. [Map  onto any one of the zeros of f onto any one of the zeros of f  , f = IrrF(x)( , f = IrrF(x)( ,X).] But then ,X).] But then  (x) = x', so that by our assumption, x' (x) = x', so that by our assumption, x'   (E) = E. (E) = E.
(4) (1). By Theorem 3 of the section of the restrictive assumption, there exist (1). By Theorem 3 of the section of the restrictive assumption, there exist   E such that E = F( E such that E = F( ). Let ). Let  1,..., 1,..., n be the conjugates of n be the conjugates of  over F. By (4), over F. By (4),  1,..., 1,..., n all belong to E, so that E = F( n all belong to E, so that E = F( 1,..., 1,..., n). Thus, E can be gotten by adjoining to F all zeros of IrrF( n). Thus, E can be gotten by adjoining to F all zeros of IrrF( ,X), so that E is a splitting field of IrrF( ,X), so that E is a splitting field of IrrF( ,X) over F. ,X) over F.
As an immediate consequence of the above result we deduce that Q( ) is not a normal extension of Q, since the conjugates ) is not a normal extension of Q, since the conjugates  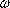 and and  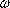 2 of 2 of  over Q are not in Q( over Q are not in Q( ), which violates condition (4). Moreover, if ), which violates condition (4). Moreover, if  m is a primitive mth root of 1, then Q( m is a primitive mth root of 1, then Q( m) is a normal extension of Q, since it is the splitting field over Q of m) is a normal extension of Q, since it is the splitting field over Q of  m(X). [The zeros of m(X). [The zeros of  m(X) are m(X) are  ma, 0 < a< m - 1, (a,m) = 1.] ma, 0 < a< m - 1, (a,m) = 1.]
|
 ,
, )
)
 E
E ).
). ,
, )
)
 E
E ).
). 1,...,
1,..., n)
n)
 E
E ).
). be an F-isomorphism of E into F. Then
be an F-isomorphism of E into F. Then  has the form (1), where
has the form (1), where  (
( )
) over F. In particular, there are at most n F-isomorphisms of E into F.
Let E1 and E2 be fields,
over F. In particular, there are at most n F-isomorphisms of E into F.
Let E1 and E2 be fields,  E2
E2 E1
E1 )
) ,X).
,X). :F
:F K
K F[X],
F[X], =
= (a0)+
(a0)+ (a1)X+...+
(a1)X+...+ (an-1)Xn-1+Xn
(an-1)Xn-1+Xn  K[X],
K[X], be any zero of f
be any zero of f  in K. Then there exists an isomorphism
in K. Then there exists an isomorphism  :F(
:F( )
) K
K to F coincides with
to F coincides with  and (2)
and (2)  (
( )=
)= .
. is an extension of
is an extension of  to F(
to F( ) which maps
) which maps  to
to  .
Let
.
Let  F[X]
F[X] be algebraic over F, n =
be algebraic over F, n =  ,X)).
,X)). )/F)
)/F) ,
, 2,...,
2,..., n-1}
n-1} )
) 1,
1, 2,...,
2,..., n)
n)
 F(
F( 1,...,
1,..., n)
n) 1,...,
1,..., n) = F(
n) = F( ).
). is algebraic over F if there exists a nonzero polynomial
is algebraic over F if there exists a nonzero polynomial  F[X]
F[X] ) = 0.
) = 0. is not algebraic over F, then we say that
is not algebraic over F, then we say that  is transcendental over F.
Let
is transcendental over F.
Let 
 E be algebraic over F.
E be algebraic over F.  the zero of a monic irreducible polynomial
the zero of a monic irreducible polynomial  F[X]
F[X] over F denoted
over F denoted  ,X)
,X) 1)(X -
1)(X -  2)...(X -
2)...(X -  n),
n),  i
i  F,
F,  1 =
1 =  .
. + ... + an-1
+ ... + an-1 n-1, ai
n-1, ai  F, n = deg(E/F).
F, n = deg(E/F). (x) =
(x) =  (a0) +
(a0) +  (a1)
(a1) (
( ) + ... +
) + ... +  (an-1)
(an-1) (
( )n-1
)n-1 (
( ) + ... + an-1
) + ... + an-1 (
( )n-1.
)n-1. + ... + bn-1
+ ... + bn-1 n-1 +
n-1 +  n
n 0 =
0 =  (0) =
(0) =  (b0 + b1
(b0 + b1 + ... + bn-1
+ ... + bn-1 n-1 +
n-1 +  n)
n) (b0) +
(b0) +  (b1)
(b1) (
( ) + ... +
) + ... +  (bn-1)
(bn-1) (
( )n-1 +
)n-1 +  (
( )n
)n (
( ) + ... + bn-1
) + ... + bn-1 (
( )n-1 +
)n-1 +  (
( )n
)n (
( )).
)). F[X],
F[X], =
=  (a0) +
(a0) +  (a1)X + ... +
(a1)X + ... +  (an-1)Xn-1 + Xn
(an-1)Xn-1 + Xn  K[X],
K[X], + ... + an-1
+ ... + an-1 n-1, ai
n-1, ai F.
F. (x) =
(x) =  (a0) +
(a0) +  (a1)
(a1) + ... +
+ ... +  (an-1)
(an-1) n-1.
n-1. + ... + bn-1
+ ... + bn-1 n-1, bi
n-1, bi  F.
F. )h(
)h( ) = r(
) = r( ).
). =
=  (e0) +
(e0) +  (e1)X + ... +
(e1)X + ... +  (es)Xs
(es)Xs  K[X],
K[X], (x · y) = r
(x · y) = r (
( )
) (
( ) · q
) · q (
( ) + r
) + r (
( )
) (
( )
) (
( )
) (
( ) · h
) · h (
( )
) (x) ·
(x) ·  (y).
(y). i(b0 + b1
i(b0 + b1 + ... + bn-1
+ ... + bn-1 n-1)
n-1) i + ... + bn-1
i + ... + bn-1 in-1, bj
in-1, bj  F.
F. 1,
1, 2},
2},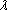 1,
1,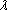 2,
2,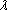 3},
3},