|
A Restrictive Assumption
Let F be a field. F its algebraic closure, f  F[X] a monic, nonconstant polynomial. In F[X], we may factor f into linear factors: F[X] a monic, nonconstant polynomial. In F[X], we may factor f into linear factors:
Suppose that m of the  i are distinct. Let us renumber i are distinct. Let us renumber  1,..., 1,..., n so that n so that  1,..., 1,..., m are all different. Then m are all different. Then
f =  (X -  i i) vi, v i > 1.
The positive integer vi is called the multiplicity of the zero  i. If vi = 1, then i. If vi = 1, then  i is called a simple zero of f; if vi > 1, then i is called a simple zero of f; if vi > 1, then  i is called a multiple zero of f. A multiplicity > 1 is called a multiple zero. i is called a multiple zero of f. A multiplicity > 1 is called a multiple zero.
An irreducible polynomial f  F[X] can have multiple zeros. For example, let F = Z2(Y), where Y is transcendental over Z2, and let f = X2 - Y F[X] can have multiple zeros. For example, let F = Z2(Y), where Y is transcendental over Z2, and let f = X2 - Y  F[X]. Then f is irreducible in F[X]. Otherwise, f factors into linear factors in F[X] and there exists Z F[X]. Then f is irreducible in F[X]. Otherwise, f factors into linear factors in F[X] and there exists Z  F such that Z2 = Y. But Z is the quotient of two polynomials in Y, so that we get an algebraic equation for Y over Z2, a contradiction to the fact that Y is transcendental over Z2. Thus, f is irreducible in F[X]. In F[X], F such that Z2 = Y. But Z is the quotient of two polynomials in Y, so that we get an algebraic equation for Y over Z2, a contradiction to the fact that Y is transcendental over Z2. Thus, f is irreducible in F[X]. In F[X],
f = (X - 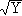 )(X + 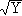 ),
where 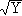 denotes a fixed square root of Y in F. But 1 + 1 = 0 in F, so that denotes a fixed square root of Y in F. But 1 + 1 = 0 in F, so that
(1 + 1) 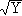 = 0 Thus,
f = (X - 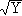 ) 2
and 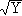 is a multiple zero of f. is a multiple zero of f.
In order to avoid this and other pathologies, let us restrict our fields somewhat. Henceforth, unless explicit mention to the contrary is made, we will assume that all fields are extensions of Q. For example. we rule out Z2(Y) since if F is an extension of Q, 1 + 1 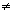 0 in F. It is possible to develop field theory somewhat more generally than we will attempt to do here. So we will develop a somewhat specialized Galois theory, for extensions of Q. In the remainder of this section, let us show what this restriction does for us. First we will prove that the phenomenon exhibited above cannot occur. 0 in F. It is possible to develop field theory somewhat more generally than we will attempt to do here. So we will develop a somewhat specialized Galois theory, for extensions of Q. In the remainder of this section, let us show what this restriction does for us. First we will prove that the phenomenon exhibited above cannot occur.
Theorem 1: Let f  F[X] be irreducible and of degree > 1. Then all zeros of f in F are simple. F[X] be irreducible and of degree > 1. Then all zeros of f in F are simple.
Before proving Theorem 1, let us introduce a few tools. Let n  N, a N, a  F. In the chapter on rings we defined n · a or the scalar product as follows: F. In the chapter on rings we defined n · a or the scalar product as follows:
n · a = 0 if n = 0,
= 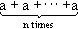 if n > 0.
If h = a0 + a1X + ... + arXr  F[X], let us define the formal derivative Dh of h by F[X], let us define the formal derivative Dh of h by
Dh = 1 · a1 + 2 · a2X + ... + r · arXr-1.
Then Dh  F[X]. It is trivial to verify the following properties of the formal derivative: F[X]. It is trivial to verify the following properties of the formal derivative:
(1)
D(ag + bh) = aDg + bDh (a,b  F F; g,h  F F[X]),
D(gh) = hDg + gDh (g,h  F F[X]),
D(x - a) v = v(x - a) v-1 (a  F F, v >1).
If deg( f ) = n, then deg(D f ) = n - 1 (n > 1, f  F F[X]).
Lemma 2: Suppose that f has a multiple zero. Then f and Df have a nonconstant factor in F[X].
Proof: If  is a multiple zero of f, then f = (x - is a multiple zero of f, then f = (x -  )vg, g )vg, g  F[X], v > 1. By (1)-(3), we have, F[X], v > 1. By (1)-(3), we have,
D f = v(X -  ) v-1g + (X -  ) vg.
But since v > 1,  is a zero of Df. If f and Df have no nonconstant common factor in F[X], then there exist is a zero of Df. If f and Df have no nonconstant common factor in F[X], then there exist  , ,  F[X] such that 1 = F[X] such that 1 =  f + f +  Df. Therefore, if we replace X by Df. Therefore, if we replace X by  in this last equation, we get 1 = 0, which is a contradiction. Thus, (f,Df) in this last equation, we get 1 = 0, which is a contradiction. Thus, (f,Df)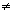 1. 1.
Proof of Theorem 1: Without loss of generality, assume that f is monic and assume that f has a multiple zero. Then deg(f ) > 2, and if deg(f ) = n, then deg(Df ) = n - 1 > 1. Moreover, by Lemma 2, (f,Df )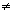 1, so that f and Df have a nontrivial factor in common. Since f is irreducible, this implies that Df is divisible by f. But this is impossible since 1 < deg(Df ) < deg(f ). 1, so that f and Df have a nontrivial factor in common. Since f is irreducible, this implies that Df is divisible by f. But this is impossible since 1 < deg(Df ) < deg(f ).
The next result is another extremely useful consequence of our restrictive assumption.
Theorem 3 (Primitive Element Theorem): Let E = F( , , ) be an algebraic extension of F. Then there exists ) be an algebraic extension of F. Then there exists   E such that E = F( E such that E = F( ). Thus, E is a simple extension of F. ). Thus, E is a simple extension of F.
Proof: Let F be the algebraic closure of F and let f = IrrF( ,X), g = IrrF( ,X), g = IrrF( ,X). Then in F, we have ,X). Then in F, we have
f = (X -  1 1)...(X -  n n),  i i  F F,  1 1 =  ,
g = (X -  1 1)...(X -  m m),  j j  F F,  1 1 =  .
Consider the following set of elements of F:
(5)
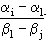 (1 < i < n, 2 < j < m).
This set is finite and, since F  Q, we can choose t Q, we can choose t  F distinct from all the elements of (5). We will prove that E = F( F distinct from all the elements of (5). We will prove that E = F( ) with ) with  = =  + t + t  E, it is clear that E E, it is clear that E  F( F( ). Let us prove the reverse inclusion. Consider the polynomial ). Let us prove the reverse inclusion. Consider the polynomial
Then h( ) = f( ) = f( - t - t ) = f( ) = f( ) = 0. Therefore, in F[X], h(X) is divisible by X - ) = 0. Therefore, in F[X], h(X) is divisible by X -  1. If h(X) is divisible by X - 1. If h(X) is divisible by X -  j for some j > 1, then h( j for some j > 1, then h( j) = 0, which implies that f( j) = 0, which implies that f( - t - t j) = 0. Therefore, j) = 0. Therefore,  - t - t j is a zero of f, and thus j is a zero of f, and thus  = t = t j = j =  i for some i. But since i for some i. But since  1 + t 1 + t 1, this implies that 1, this implies that
t = 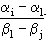 ,
which contradicts the choice of t. Thus h(X) is divisible by X -  1, but not by X - 1, but not by X -  j for j > 1. Therefore, in F[X], the g.c.d. of h(X) and g(X) is X - j for j > 1. Therefore, in F[X], the g.c.d. of h(X) and g(X) is X -  1, and consequently, in F( 1, and consequently, in F( )[X],, the g.c.d. of h(X) and g(X) is either 1 or X - )[X],, the g.c.d. of h(X) and g(X) is either 1 or X -  1. If it were 1, then there exists a(X), b(X) 1. If it were 1, then there exists a(X), b(X)  F( F( )[X] such that a(X)h(X) + b(X)g(X) = 1. Setting X = )[X] such that a(X)h(X) + b(X)g(X) = 1. Setting X =  1, we then get 0 = 1, a contradiction. Therefore, the g.c.d of h(X) and g(X) in F( 1, we then get 0 = 1, a contradiction. Therefore, the g.c.d of h(X) and g(X) in F( )[X] is X - )[X] is X -  1. In particular, 1. In particular,  1 1  F( F( ). But then ). But then  = =  1t = 1t =   F( F( ), so that F( ), so that F( , , ) )  F( F( ). This completes the proof of the theorem. ). This completes the proof of the theorem.
Corollary 4: Let F( 1, 1, 2,..., 2,..., n) be an algebraic extension of F. Then there exists n) be an algebraic extension of F. Then there exists   F( F( 1,..., 1,..., n) such that F( n) such that F( 1,..., 1,..., n) = F( n) = F( ). ).
Proof: Induction on n.
|
 F[X]
F[X] F[X]
F[X]
 E be algebraic over F.
E be algebraic over F.  the zero of a monic irreducible polynomial
the zero of a monic irreducible polynomial  F[X]
F[X] over F denoted
over F denoted  ,X)
,X) is algebraic over F if there exists a nonzero polynomial
is algebraic over F if there exists a nonzero polynomial  F[X]
F[X] ) = 0.
) = 0. is not algebraic over F, then we say that
is not algebraic over F, then we say that  is transcendental over F.
If f has a leading coefficient 1, then we say that f is monic.
A field is a nontrivial commutative ring with identity in which every nonzero element has an inverse with respect to multiplication.
A field F is said to be algebraically closed if every nonconstant polynomial if F[X] splits into a product of linear factors in F[X].
is transcendental over F.
If f has a leading coefficient 1, then we say that f is monic.
A field is a nontrivial commutative ring with identity in which every nonzero element has an inverse with respect to multiplication.
A field F is said to be algebraically closed if every nonconstant polynomial if F[X] splits into a product of linear factors in F[X].
 (X -
(X -  i)vi, vi > 1.
i)vi, vi > 1.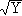 )(X +
)(X + 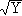 ),
),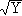 = 0
= 0
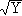 = -
= -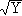 .
.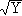 )2
)2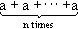 if n > 0.
if n > 0. F[X]),
F[X]), F, v >1).
F, v >1). F[X]).
F[X]). )v-1g + (X -
)v-1g + (X -  )vg.
)vg.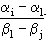 (1 < i < n, 2 < j < m).
(1 < i < n, 2 < j < m). - tX)
- tX)  F(
F( )[X].
)[X].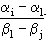 ,
,