Algebraic and Transcendental Elements
Throughout this section let F be a field and E an extension of field F. Let us begin by classifying the elements of E into two broad categories with respect to F. Let   E. We say that E. We say that  is algebraic over F if there exists a nonzero polynomial f is algebraic over F if there exists a nonzero polynomial f  F[X] such that f( F[X] such that f( ) = 0. If ) = 0. If  is not algebraic over F, then we say that is not algebraic over F, then we say that  is transcendental over F. In order to get some feel for this classification, let us study some examples. is transcendental over F. In order to get some feel for this classification, let us study some examples.
Example 1:   F F   is algebraic over F. For is algebraic over F. For  is a zero of X - is a zero of X -   F[X]. F[X].
Example 2: Let F = Q, E = C. Then  1 = 1 =  , ,  2 = 2 =  , ,  3 = 3 =  + +  are all algebraic over Q. For are all algebraic over Q. For  1 is a zero of X2 - 2; 1 is a zero of X2 - 2;  2 is a zero of X3 - 7; 2 is a zero of X3 - 7;  3 is a zero of X6 - 6X4 - 14X3 + 12X2 - 84X + 41. 3 is a zero of X6 - 6X4 - 14X3 + 12X2 - 84X + 41.
Example 3: Let F = Q, E = C. Then  = 3.1415926..., e = 2.718281... are transcendental over Q. We cannot come near to proving these two assertions here. Both are celebrated results of nineteenth-century mathematics. It was long suspected that neither = 3.1415926..., e = 2.718281... are transcendental over Q. We cannot come near to proving these two assertions here. Both are celebrated results of nineteenth-century mathematics. It was long suspected that neither  nor e can satisfy a polynomial equation with rational coefficients. However, the transcendentality of nor e can satisfy a polynomial equation with rational coefficients. However, the transcendentality of  was not proved until 1882, when it was settled by Lindemann. The transcendentality of e is somewhat easier and was first proved by Hermite in 1873. was not proved until 1882, when it was settled by Lindemann. The transcendentality of e is somewhat easier and was first proved by Hermite in 1873.
Example 4: The theory of transcendental numbers is a vast realm of mathematics in which research is still going on in many parts of the mathematical community. It is an extremely difficult branch of mathematics, which relies for many of its proofs on analysis, especially on functions of a complex variable. Some apparently very simple questions on transcendence cannot be answered at the present time. Although we cannot go into an extended discussion of the theory of transcendental numbers, let us cite one of the crowning achievements of the theory, the Gelfond-Schneider theorem:
Theorem 1: Let   0, 1 be algebraic over Q. Let 0, 1 be algebraic over Q. Let  be algebraic over Q, be algebraic over Q,   Q. Then Q. Then   is transcendental over Q. is transcendental over Q.
Thus, for example, 2 is transcendental over Q. The statement of this theorem was first guessed by Euler in the eighteenth century as was posed by Hilbert as one of his famous 23 problems at the International Congress of Mathematics in Paris in 1900. A proof of the result was discovered almost simultaneously in 1934 by Gelfond and Schneider, working independently. is transcendental over Q. The statement of this theorem was first guessed by Euler in the eighteenth century as was posed by Hilbert as one of his famous 23 problems at the International Congress of Mathematics in Paris in 1900. A proof of the result was discovered almost simultaneously in 1934 by Gelfond and Schneider, working independently.
We have not given any examples of transcendental elements which we could actually show to be transcendental. There is one obvious example however:
Example 5: Let F be a field, X an indeterminate over F. Let F(X) be the quotient field of F[X]. Then F(X) is an extension field of F, so we may set E = F(X). Then X  E is transcendental over f. For if X satisfies the polynomial equation with coefficients in F, then E is transcendental over f. For if X satisfies the polynomial equation with coefficients in F, then
c nX n + c n-1X n-1 + ... + c 0 c i  F
 c 0 = c 1 = ... = c n = 0
since X is an indeterminate over F. Thus, X cannot be the zero of any nonzero polynomial with coefficients in F.
In the remainder of this work we will have little to say concerning transcendental elements. This is for at least two reasons. First, the theory of transcendental numbers is far too complicated for the scope of this work. Second, we are striving toward a theory of polynomial equations. And zeros of a polynomial are algebraic over any field containing the coefficients of the polynomial.
Let   E be algebraic over F. Our first task is to single out a single polynomial having E be algebraic over F. Our first task is to single out a single polynomial having  as a zero. Let f as a zero. Let f  F[X] have F[X] have  as a zero. Since F[X] is a UFD, we may write f = p1,...,pn, where pi as a zero. Since F[X] is a UFD, we may write f = p1,...,pn, where pi  F[X] is irreducible. Then F[X] is irreducible. Then
But since E is an integral domain and p1( ) )  E (1 < i < r), we see that pi( E (1 < i < r), we see that pi( ) = 0 for some i. Thus, ) = 0 for some i. Thus,  is a zero of some irreducible polynomial p is a zero of some irreducible polynomial p  F[X]. Without loss of generality, we may normalize p to be monic. We assert that p is the unique monic, irreducible polynomial in F[X] having F[X]. Without loss of generality, we may normalize p to be monic. We assert that p is the unique monic, irreducible polynomial in F[X] having  as a zero. Indeed if q were another such polynomial, then p and q are relatively prime, so that there exist polynomials a, b as a zero. Indeed if q were another such polynomial, then p and q are relatively prime, so that there exist polynomials a, b  F[X] such that ap + bq = 1. But then F[X] such that ap + bq = 1. But then
which is a contradiction. Then polynomial p is called the irreducible polynomial of  over F and is denoted IrrF( over F and is denoted IrrF( ,X). Moreover, the manner in which we constructed p implies ,X). Moreover, the manner in which we constructed p implies
Lemma 2: Let   E be algebraic over F, and let f E be algebraic over F, and let f  F[X] be such that f( F[X] be such that f( ) = 0. Then f is divisible by IrrF( ) = 0. Then f is divisible by IrrF( ,X). ,X).
Example 6: X2 - 2 is monic and irreducible in Q[X]. Therefore, IrrQ( , X) = X2 - 2. , X) = X2 - 2.
Example 7: Let d  Z not be a perfect square. Then X2 - d is monic and irreducible in Q[X], so that IrrQ( Z not be a perfect square. Then X2 - d is monic and irreducible in Q[X], so that IrrQ( ,X) = X2 - d. ,X) = X2 - d.
Example 8: Let   F. Then IrrF( F. Then IrrF( ,X) = X - ,X) = X -  . .
As the reader may have already guessed, it is often relatively easy to exhibit a polynomial f  F[X] for which f( F[X] for which f( ) = 0. The difficult part of constructing IrrF( ) = 0. The difficult part of constructing IrrF( ,X) is to make sure that f is irreducible. There is a reasonable way of going about this, at least in the case F = Q. If we can exhibit some f ,X) is to make sure that f is irreducible. There is a reasonable way of going about this, at least in the case F = Q. If we can exhibit some f  F[X] such that f( F[X] such that f( ) = 0, then we can try to factor f and determine an irreducible factor of f which has ) = 0, then we can try to factor f and determine an irreducible factor of f which has  as a zero. The irreducibility developed in the previous chapters are useful in proving that a given factor of f is irreducible. Particular attention should be called to the Eisenstein irreducibility criterion. as a zero. The irreducibility developed in the previous chapters are useful in proving that a given factor of f is irreducible. Particular attention should be called to the Eisenstein irreducibility criterion.
If E is an extension of the field F, then E may be regarded as a vector space over F. The product  ·v of a scalar ·v of a scalar   F and a vector v F and a vector v  E is just the product of E is just the product of  and v, considered as elements of E. The dimension of E over F is called the degree of E over F, denoted deg(E/F). and v, considered as elements of E. The dimension of E over F is called the degree of E over F, denoted deg(E/F).
For example, we showed in a previous section that
Therefore, {1, } generates Q( } generates Q( ) over Q. Moreover, {1, ) over Q. Moreover, {1,  } is linearly independent over Q, since if a + b } is linearly independent over Q, since if a + b = 0 with a,b not both 0, we see that b = 0 with a,b not both 0, we see that b 0, so that 0, so that  = -a/b = -a/b  Q, which contradicts the fact that Q, which contradicts the fact that  is irrational. Thus we see that {1, is irrational. Thus we see that {1, } is a basis of Q( } is a basis of Q( ) over Q and that deg(Q ) over Q and that deg(Q /Q) = 2. Note that IrrQ( /Q) = 2. Note that IrrQ( ,X) = X2 - 2 and that deg(IrrQ( ,X) = X2 - 2 and that deg(IrrQ( ,X)) = deg(Q ,X)) = deg(Q )/Q). This phenomenon is not accidental as the following result shows. )/Q). This phenomenon is not accidental as the following result shows.
Theorem 3: Let  be algebraic over F, n = deg(IrrF( be algebraic over F, n = deg(IrrF( ,X)). Then ,X)). Then
(1) deg(F( )/F) = n. )/F) = n.
(2) {1, , , 2,..., 2,..., n-1} is a basis for F( n-1} is a basis for F( ) over F. ) over F.
Proof: Since {1, , , 2,..., 2,..., n-1} contains n elements, it is clear that part (2) implies part (1). To prove part (2), we must show that every n-1} contains n elements, it is clear that part (2) implies part (1). To prove part (2), we must show that every   F( F( ) can be written uniquely in the form ) can be written uniquely in the form
(1)
 = a 0· 1 + a 1·  + ... + a n-1 n-1 n-1 (a i  F).
The uniqueness is simple. For if  = a0'·1 + a1' = a0'·1 + a1' + an-1' + an-1' n-1, then n-1, then
(a 0-a 0') + (a 1 - a 1')  + ... + (a n-1 - a n-1')  n-1 n-1 = 0.
But then the polynomial f = (a0-a0') + (a1 - a1')X + ... + (an-1 - an-1')Xn-1 has  as a zero. Therefore, by Lemma 2, f is divisible by IrrQ( as a zero. Therefore, by Lemma 2, f is divisible by IrrQ( ,X). where the later has degree n. Thus, we are forced to conclude that f = 0, which implies that a0 = a0', a1 = a1', ..., an-1 = an-1', which gives us the uniqueness of the representation (1). Let us now show that every ,X). where the later has degree n. Thus, we are forced to conclude that f = 0, which implies that a0 = a0', a1 = a1', ..., an-1 = an-1', which gives us the uniqueness of the representation (1). Let us now show that every   F( F( ) can be written in the form (1). Let F[ ) can be written in the form (1). Let F[ ] denote the smallest subring of F( ] denote the smallest subring of F( ) containing F and ) containing F and  . Then F[ . Then F[ ] consists of all sums of the form ] consists of all sums of the form
(2)
a 0 + a 1 + ... + a m m m (a i  F).
We assert that every sum of the form(2) can be rewritten in the form
(3)
b 0 + b 1 + ... + b n-1 n-1 n-1 (b i  F).
It clearly suffices to show that ar (r > n) can be so written. Let us proceed by induction on r. Let
IrrF(  ,X) = X n + c n-1X n-1 + ... + c 0.
Then  n = -cn-1 n = -cn-1 n-1-cn-2 n-1-cn-2 n-2-...-c0, so n-2-...-c0, so  n can be written in the form (3). Thus the assertion is true for r = n. Assume that r > n and that n can be written in the form (3). Thus the assertion is true for r = n. Assume that r > n and that  r-1 can be written in the form (3). Then r-1 can be written in the form (3). Then
 r r =  ·  r-1 r-1 =  ·(b 0 + b 1 + ... + b n-1 n-1 n-1)
= b 0' + b 1'  + ... + b n-1 n-1 n-1,
since  n can be written in the form of (3). Thus, the induction is complete. We have shown that n can be written in the form of (3). Thus, the induction is complete. We have shown that
(4)
F[  ] = {a 0 + a 1 + ... + a n-1 n-1 n-1 | a i  F}.
It is clear that F[ ] contains both F and ] contains both F and  and F[ and F[ ] ] F( F( ). Therefore, if we prove that F[ ). Therefore, if we prove that F[ ] is a field, then we can conclude that F[ ] is a field, then we can conclude that F[ ] ]  F( F( ) and therefore F[ ) and therefore F[ ] = F( ] = F( ). Therefore by (4) we conclude that every ). Therefore by (4) we conclude that every   F( F( ) can be in the form (2). Thus we must show that F[ ) can be in the form (2). Thus we must show that F[ ] is a field. Let ] is a field. Let
be the homomorphism "evaluation at  ." Then it is easy to see that ." Then it is easy to see that   is surjective. Moreover, ker( is surjective. Moreover, ker(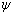  ) = g · F[X], where g - IrrF( ) = g · F[X], where g - IrrF( ,X). Therefore, ,X). Therefore,
F[X]/g · F[X] 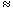 F[  ].
However, since g is irreducible, g · F[X] is a maximal ideal by Example 5 in the section on maximal ideals and thus F[X]/g · F[X] is a field by Theorem 8 of the section on maximal ideals. Thus, F[ ] is a field, since the image under a field under an isomorphism again a field. ] is a field, since the image under a field under an isomorphism again a field.
In Theorem 3, we described the simple extension F( ) in case ) in case  is algebraic over F. Let us now carry out the correspondence task in case is algebraic over F. Let us now carry out the correspondence task in case  is transcendental over F. The clue is provided by example 5. is transcendental over F. The clue is provided by example 5.
Proposition 4: Let F( ) be a simple extension of F ant let ) be a simple extension of F ant let  be transcendental over F. Then the mapping be transcendental over F. Then the mapping
p(X)/q(X)  p(  )/q(  ) (p(X),q(X)  F[X], q(X)  0 0)
is a surjective F-isomorphism. In particular, F(X) and F( ) are F-isomorphic. ) are F-isomorphic.
Proof: First note that q( ) ) 0 since 0 since  is transcendental over F and q(X) is transcendental over F and q(X) 0. Thus, p( 0. Thus, p( )/q( )/q( ) makes sense. Second, let us show that ) makes sense. Second, let us show that 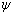 is well defined: If p1(X)/q1(X) = p2(X)/q2(X), then is well defined: If p1(X)/q1(X) = p2(X)/q2(X), then
p1(X)q2(X) = q1(X)p2(X),
Thus, 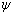 is well defined. It is easy to check that is well defined. It is easy to check that 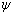 is a ring homomorphism. Therefore, by Proposition 2 of the introduction to fields, is a ring homomorphism. Therefore, by Proposition 2 of the introduction to fields, 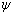 is an isomorphism since is an isomorphism since 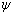 is not identically zero. By (5) of the intro, is not identically zero. By (5) of the intro, 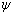 is surjective. is surjective.
We showed in Theorem 3 that if  is algebraic over F, then deg(F( is algebraic over F, then deg(F( )/F) = deg(IrrF( )/F) = deg(IrrF( ,X)). In particular, deg(F( ,X)). In particular, deg(F( )/F) is finite. The situation is quite different if )/F) is finite. The situation is quite different if  is transcendental over F, however. Indeed, the set is transcendental over F, however. Indeed, the set
{1,  ,  2 2, ...} = S
is then an infinite, linearly independent subset of F( ). For if ). For if
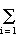 a i i i = 0, a i  F, a i not all 0,
is a linear relation among the elements of S, then  is the zero of some nonzero polynomial with coefficients in F, a contradiction to the assumption that is the zero of some nonzero polynomial with coefficients in F, a contradiction to the assumption that  is transcendental over F. Thus if is transcendental over F. Thus if  is transcendental over F, deg(F( is transcendental over F, deg(F( )/F) is finite. If E is an extension field of F, then we say that E is a finite extension of F (or that E/F is finite) if deg(E/F) is finite. Thus we have proved the following result: )/F) is finite. If E is an extension field of F, then we say that E is a finite extension of F (or that E/F is finite) if deg(E/F) is finite. Thus we have proved the following result:
Theorem 5: F( )/F is finite if and only if )/F is finite if and only if  is algebraic over F. is algebraic over F.
|

 E be algebraic over F.
E be algebraic over F.  the zero of a monic irreducible polynomial
the zero of a monic irreducible polynomial  F[X]
F[X] over F denoted
over F denoted  ,X)
,X)
 E be algebraic over F.
E be algebraic over F.  the zero of a monic irreducible polynomial
the zero of a monic irreducible polynomial  F[X]
F[X] over F denoted
over F denoted  ,X)
,X) E2
E2 E1
E1 Z[X]
Z[X] an,
an, a0.
a0. Let
Let 
 E
E F[X]
F[X] ) = 0.
) = 0. ,X).
,X).
 iei
iei B
B B
B A
A is algebraic over F if there exists a nonzero polynomial
is algebraic over F if there exists a nonzero polynomial  F[X]
F[X] ) = 0.
) = 0. is not algebraic over F, then we say that
is not algebraic over F, then we say that  is transcendental over F.
A commutative ring R is an integral domain if R contains no zero divisors. In other words, R is an integral domain if the product of any two nonzero elements of R is nonzero.
The set of rational numbers.
The set integers.
Let R be an integral domain. There exists a field FR and an embedding
is transcendental over F.
A commutative ring R is an integral domain if R contains no zero divisors. In other words, R is an integral domain if the product of any two nonzero elements of R is nonzero.
The set of rational numbers.
The set integers.
Let R be an integral domain. There exists a field FR and an embedding  FR
FR R, b
R, b 0).
0). Rx
Rx Rx
Rx 1 ...
1 ...  s =
s =  1 ...
1 ... 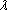 t
t 1 ...
1 ...  s
s 1 and
1 and 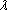 1 are associates
1 are associates  H is a homomorphism. The kernel of f is ker(f) = {x
H is a homomorphism. The kernel of f is ker(f) = {x  G | f(x) = 1H}.
G | f(x) = 1H}.
 F
F c0 = c1 = ... = cn = 0
c0 = c1 = ... = cn = 0 ) = p1(
) = p1( )...pr(
)...pr( ).
). )p(
)p( ) + b(
) + b( )q(
)q( ) = 1,
) = 1, = a0·1 + a1·
= a0·1 + a1· + ... + an-1
+ ... + an-1 n-1 (ai
n-1 (ai  F).
F). + ... + (an-1 - an-1')
+ ... + (an-1 - an-1') n-1 = 0.
n-1 = 0. + ... + am
+ ... + am m (ai
m (ai  F).
F). + ... + bn-1
+ ... + bn-1 n-1 (bi
n-1 (bi  F).
F). ,X) = Xn + cn-1Xn-1 + ... + c0.
,X) = Xn + cn-1Xn-1 + ... + c0. r =
r =  ·
· r-1 =
r-1 =  ·(b0 + b1
·(b0 + b1 + ... + bn-1
+ ... + bn-1 n-1)
n-1) + b1
+ b1 2 + ... + bn-1
2 + ... + bn-1 n
n + ... + bn-1
+ ... + bn-1 n-1,
n-1, ] = {a0 + a1
] = {a0 + a1 + ... + an-1
+ ... + an-1 n-1 | ai
n-1 | ai  F}.
F}.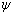
 : F[X]
: F[X] F[
F[ ]
]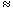 F[
F[ ].
].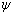 : F(X)
: F(X)  F(
F( ),
), p(
p( )/q(
)/q( ) (p(X),q(X)
) (p(X),q(X)  F[X], q(X)
F[X], q(X) 0)
0)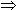 p1(
p1( )q2(
)q2( ) = q1(
) = q1( )p2(
)p2( ),
),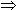 p1(
p1( )/q1(
)/q1( ) = p2(
) = p2( )/q2(
)/q2( ),
), ,
, 2, ...} = S
2, ...} = S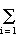 ai
ai i = 0, ai
i = 0, ai  F, ai not all 0,
F, ai not all 0,