Splitting Fields
We can construct the complex numbers C by adjoining to R a zero of the polynomial X2 + 1 in R[X]. Let us now take up the general problem of adjoining to F a zero of some polynomial f  F[X], where F is an arbitrary field. Throughout this section, let F[X], where F is an arbitrary field. Throughout this section, let
f = X n + a n-1X n-1 + ... + a 0, a i  F.
Let us first obtain some information about what zeros f can have in an extension E of F. (The case E = F is not excluded.) Our first result is a generalization of a well-known example from high school algebra.
Proposition 1: Let   E. Then E. Then  is a zero of f if and only if X - is a zero of f if and only if X -  divides f in E[X]; that is, f = (X - divides f in E[X]; that is, f = (X -  )g for some g )g for some g  E[X]. E[X].
Proof: By the division algorithm in E[X], we may write
f = (X -  )g + r, g,r  E[X],
where r = 0 or 0 < deg(r) < 1. In either case, r is a constant polynomial, say r =   E, so that f = (X - E, so that f = (X -  ) g + ) g +  . Evaluating f at . Evaluating f at  , we see that , we see that
f(  ) =  ,
and therefore f = (X -  )g + f( )g + f( ). Thus, f( ). Thus, f( ) = 0 if and only if X - ) = 0 if and only if X -  divides f in E[X]. divides f in E[X].
Corollary 2: f has at most n zeros in E.
Proof: Let  1,..., 1,..., k be distinct zeros of f in E. Then, in E[X], f is divisible by (X- k be distinct zeros of f in E. Then, in E[X], f is divisible by (X- 1)(X - 1)(X -  2)···(X - 2)···(X -  k). Therefore, n > k. k). Therefore, n > k.
Corollary 3: Suppose that n > 1 and f is irreducible in E[X]. Then f has no zeros in E.
Proof: For if f has a zero  in E, then f is divisible by X - in E, then f is divisible by X -  in E[X], so that f is reducible in E[X] (since n > 1). in E[X], so that f is reducible in E[X] (since n > 1).
Let us now prove the main result of this section.
Theorem 4: There exists and extension E of F which contains a zero of f.
Proof: If f1 is an irreducible factor of f in F[X], then every zero of f1 is also a zero of f. Therefore, without loss of generality, let us assume that f is irreducible in F[X]. Then I = f · F[X] is a maximal ideal of F[X], so that by Theorem 8 of the section on prime ideals, F[X]/I is a field. Since f is irreducible, f is not constant. Therefore, the mapping
F  F[X]/I,
a  a + I
is an isomorphism. Thus, let us identify F with the subring {a + I | a  F} of F[X]/I, so that we can view F[X]/I as an extension of F. Let E = F[X]/I and set F} of F[X]/I, so that we can view F[X]/I as an extension of F. Let E = F[X]/I and set  = X + I = X + I  E. Then E. Then
f(  ) = f(X) + I
= 0 + I [since f(X) = f  I],
so that  is a zero of f in E. is a zero of f in E.
A an easy consequence or Theorem 4 we deduce
Corollary 5: There exists and extension E of F such that, in E[X]. f(X) can be written in the form
Proof: By Theorem 4, there exists an extension E1 of F in which f(X) has a zero  1. By Proposition 1, f(X) is divisible by X - 1. By Proposition 1, f(X) is divisible by X -  1 in E1[X]. Therefore. there exists a monic polynomial g1(X) 1 in E1[X]. Therefore. there exists a monic polynomial g1(X)  E1[X] such that f(X) = (X - E1[X] such that f(X) = (X -  1)g1(X). Applying the same reasoning to g1(X) that we just applied to f(X), we see that there exists an extension E2 of E1, 1)g1(X). Applying the same reasoning to g1(X) that we just applied to f(X), we see that there exists an extension E2 of E1,  2 2  E2 and g2(X) such that g1(X) = (X - E2 and g2(X) such that g1(X) = (X -  2)g2(X). Therefore, f(X) = (X - 2)g2(X). Therefore, f(X) = (X -  1)(X - 1)(X -  2)g2(X). Proceeding this way, we can construct an extension En of F such that 2)g2(X). Proceeding this way, we can construct an extension En of F such that
f = g n(X) 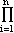 (X -  i i), g n(X)  E n[X].
But since n = deg f(X), deg gn(X) = 0, so that gn(X)  En. However, because f is monic, gn(X) = 1. Therefore, we may set E = En. En. However, because f is monic, gn(X) = 1. Therefore, we may set E = En.
Let E denote an extension of F such that
The subfield F( 1,..., 1,..., n) of E gotten by adjoining all zeros of f(X) to F is called the splitting field of f. It is clear that F( n) of E gotten by adjoining all zeros of f(X) to F is called the splitting field of f. It is clear that F( 1,..., 1,..., n) is the smallest subfield of E in which f(X) splits into a product of linear factors, whence the name "splitting field." An arbitrary field in which f(X) factors into linear factors is called a root field. If no proper subfield of the root field exists, it is the splitting field. n) is the smallest subfield of E in which f(X) splits into a product of linear factors, whence the name "splitting field." An arbitrary field in which f(X) factors into linear factors is called a root field. If no proper subfield of the root field exists, it is the splitting field.
A simple argument utilizing Corollary 5 allows us to show
Corollary 6: Let f1(X), f2(X),..., fr(X), be monic polynomials belonging to F[X] such that deg f(X) > 1 (1 < i < r). Then there exists an extension E of F such that in E[X], each polynomial f1(X) splits into a product of linear factors.
|

 E.
E. is a zero of f if and only if
is a zero of f if and only if 
 )g
)g E[X].
E[X].
 E.
E. is a zero of f if and only if
is a zero of f if and only if 
 )g
)g E[X].
E[X]. F.
F. )g + r, g,r
)g + r, g,r  E[X],
E[X], ) =
) =  ,
, F[X]/I,
F[X]/I, a + I
a + I ) = f(X) + I
) = f(X) + I I],
I],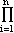 (X -
(X -  i),
i),  i
i  E.
E.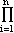 (X -
(X -  i), gn(X)
i), gn(X)  En[X].
En[X].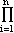 (X -
(X -  i),
i),  i
i E.
E.