|
Introduction to the Theory of Fields
If E is a field, then a subfield of E is a subset of E which is also a field with respect to the operations of E. For example, Q is a subfield of R. If F is a subfield of E, then we say that E is an extension field of F (or simply an extension of F). Thus, R is an extension of Q. Our point of view will be roughly as follows: For a given field F, we will study the properties of extensions of F. The reason for this will become apparent as we proceed. First let us consider some nontrivial examples of extensions.
Consider the set of all real numbers of the form
(1)
where the denominator is nonzero. It is reasonably apparent that the set of all such quotients is a field containing Q and  . Let us denote this field by Q( . Let us denote this field by Q( ). If F is a subfield of R which contains Q and ). If F is a subfield of R which contains Q and  , then F must contain every real number of the form (1), so that F , then F must contain every real number of the form (1), so that F  Q( Q( ). Therefore, Q( ). Therefore, Q( ) is the smallest subfield of R containing Q and ) is the smallest subfield of R containing Q and  . In particular, Q( . In particular, Q( ) is an extension of Q. Let us examine this extension more closely. Since ) is an extension of Q. Let us examine this extension more closely. Since  2 = 2, we have 2 = 2, we have  3 = 2 3 = 2 , ,  4 = 22,... Therefore, every quotient of the form (1) can be written in the form 4 = 22,... Therefore, every quotient of the form (1) can be written in the form
(2)
But since ( + + 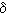  )-1 = ( )-1 = ( - - 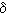  )/( )/( 2 + 2 2 + 2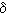 2), we see that every element of Q( 2), we see that every element of Q( ) is of the form ) is of the form
(3)
a + b  , a,b  Q Q.
Conversely, every element of the form (3) belongs to Q( ). Therefore, ). Therefore,
(4)
Let us generalize the above example into a general procedure for constructing extensions. Let F be a field, E and extension of F, S a set of elements of E. Further let 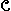 denote the collection of all subfields of E which contain F and S. Then denote the collection of all subfields of E which contain F and S. Then
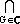 G
is a subfield of E containing F and S, and is the smallest such subfield. Let us denote this subfield by F(S). Then F(S) is called the field obtained by adjoining the elements of S to F In the above example F = Q, E = R, S ={ }. In case S = {a1, ..., an}, we will write F(a1,...,an) instead of F({a1,...,an}). A field of the form F(S) is an extension of F. Moreover, if E is an extension of F, then E = F(S) for S = E. Therefore, every extension of F can be obtained by adjoining a set of elements to F. And thus, in order to study the properties of extensions of F, we must study this process adjunction more closely. }. In case S = {a1, ..., an}, we will write F(a1,...,an) instead of F({a1,...,an}). A field of the form F(S) is an extension of F. Moreover, if E is an extension of F, then E = F(S) for S = E. Therefore, every extension of F can be obtained by adjoining a set of elements to F. And thus, in order to study the properties of extensions of F, we must study this process adjunction more closely.
Proposition 1: Let F be a field, E an extension of F, S a subset of E. If S = S1  S2, then S2, then
F(S) = F(S1)F(2).
That is, F(S) can be obtained by adjoining the elements of S2 to F(S1).
Proof: F(S1)(S2) is a subfield of E containing F(S1) and S2, so that F(S1)(S2), contains F, S1, and S2. In particular, F(S1)(S2) is a subfield of E containing F and S1  S2 = S. Therefore, F(S1)(S2) S2 = S. Therefore, F(S1)(S2)  F(S). Since S F(S). Since S  S1, S S1, S  S2, we see that F(S) S2, we see that F(S)  F(S1), F(S) F(S1), F(S)  S2. Therefore F(S) S2. Therefore F(S)  F(S1)(S2). Thus we have F(S) = F(S1)(S2). F(S1)(S2). Thus we have F(S) = F(S1)(S2).
If S = {a1,...,an}, then Proposition 1 implies that F(a1,...,an) = F(a1,...,an-1)(an). Therefore, we can reduce the process of adjoining n elements to F to n successive adjunctions of a single element: First we adjoin a1 to F; then we adjoin a2 to F(a1); then a3 to F(a1,a2); and so on. An extension of F of the form F(a) is called a simple extension of F. We have just shown that we can adjoin a set of n elements to F by forming n consecutive simple extensions. Thus, the simple extensions of a field F should be studied more closely. For now let us be content to observe that F(a) consists of all quotients of the form
(5)
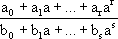 , a i,b j  F,
where the denominator is nonzero. The proof is identical to the argument we used for Q( ) above. We will examine the simple extensions to a greater extent in the next section. ) above. We will examine the simple extensions to a greater extent in the next section.
We still must supply an answer to the question: Why should we study extensions of a field? Let us answer this question by constructing a very important class of extensions of Q. If f  Q[X] is a nonconstant, monic polynomial of degree n, then f (to be more thoroughly demonstrated later) has zeros Q[X] is a nonconstant, monic polynomial of degree n, then f (to be more thoroughly demonstrated later) has zeros  1,..., 1,..., in C such that in C such that
f = (X -  1 1)(X -  2 2)···(X -  n n).
Let us form the extension Q( 1, 1, 2,..., 2,..., n) of Q. One of our major tasks is to get information about n) of Q. One of our major tasks is to get information about  1,..., 1,..., n. We will accomplish this by studying the algebraic properties of the extension Q( n. We will accomplish this by studying the algebraic properties of the extension Q( 1, 1, 2,..., 2,..., n). n).
In studying field extensions, it will be necessary to study isomorphisms of one field to another. Therefore, let us clarify the notion of isomorphism we have in mind. If E1 and E2 are fields, then an isomorphism f :E1 E2 is a ring isomorphism of E1 into E2. Thus, an isomorphism f :E1 E2 is a ring isomorphism of E1 into E2. Thus, an isomorphism f :E1 E2 is injective and preserves sums, differences, and products. But it is easy to see that if a E2 is injective and preserves sums, differences, and products. But it is easy to see that if a  E1x, we have f(a-1) = f(a)-1. E1x, we have f(a-1) = f(a)-1.
Proposition 2: Let E1 and E2 be fields, f :E1 E2 a ring homomorphism. Then either f(x) = 0 for all x E2 a ring homomorphism. Then either f(x) = 0 for all x  E1 or f is an isomorphism. E1 or f is an isomorphism.
Proof: Since E1 is a field, the only ideals of E1 are {0} and E1. But ker(f) is an ideal of E1. If ker(f) = E1, then f(x) = 0 for all x  E1. If ker(f) = {0}, then f is an isomorphism. E1. If ker(f) = {0}, then f is an isomorphism.
|
 I,
I, R,
R, I
I I.
I.
 I,
I, R,
R, I
I I.
If f:G
I.
If f:G H is a homomorphism. The kernel of f is ker(f) = {x
H is a homomorphism. The kernel of f is ker(f) = {x  G | f(x) = 1H}.
Let G and H be groups. A function
G | f(x) = 1H}.
Let G and H be groups. A function  H
H G
G B
B
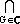 G
G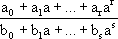 , ai,bj
, ai,bj  F,
F, 1)(X -
1)(X -  2)···(X -
2)···(X -  n).
n).