If an and bn for 1 < m < n are algebraic numbers such that {ln an, 1 < m < n} are linearly independent over Q, then
b1ln a1+ b2ln a2+ ... + bnln an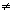 0.
0.
| Back | Table of Contents |
Aleksandr Gelfond taught mathematics at the Moscow Technological College (1929-30) and then from 1931 at Moscow State University where he held chairs of analysis, theory of numbers and the history of mathematics.
In addition to his important work in the number theory of transcendental numbers (that is, numbers that are not the solution of an algebraic equation with rational coefficients) Gelfond made significant contributions to the theory of interpolation and the approximation of functions of a complex variable.
In 1929 he conjectured that:-
If an and bn for 1 < m < n are algebraic numbers such that {ln an, 1 < m < n} are linearly independent over Q, then
b1ln a1+ b2ln a2+ ... + bnln an0.
In 1934 Gelfond proved a special case of his conjecture namely that ab is transcendental if a is algebraic (a  0, 1) and b is an irrational algebraic number. This result is now known as Gelfond's theorem and solved Problem 7 of the list of Hilbert 23 problems. It was solved independently by Schneider.
0, 1) and b is an irrational algebraic number. This result is now known as Gelfond's theorem and solved Problem 7 of the list of Hilbert 23 problems. It was solved independently by Schneider.
In 1966 A Baker proved Gelfond's Conjecture in general.
Gelfond's major contributions to transcendental numbers are in Transtendentnye i algebraicheskie chisla (1952) and to approximation and interpolation theories are in Ischislenie konechnykh raznostey (1952).
| Back | Table of Contents |