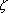 is a primitive nth root of 1, then
is a primitive nth root of 1, then 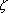 )/Q) =
)/Q) =  (n).
(n).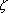 is a primitive nth root of 1, then
is a primitive nth root of 1, then 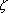 )/Q) =
)/Q) =  (n).
(n). Z[X]
Z[X] an,
an, a0.
a0.
 E be algebraic over F.
E be algebraic over F.  the zero of a monic irreducible polynomial
the zero of a monic irreducible polynomial  F[X]
F[X] over F denoted
over F denoted  ,X)
,X) :n
:n
 (n) = the number of integers a (1 < a < n) such that
(n) = the number of integers a (1 < a < n) such that  F
F  G
G 1,...,
1,..., n} is a basis of G over F and {
n} is a basis of G over F and { 1,...,
1,..., m} is a basis of F over E, then {
m} is a basis of F over E, then { i
i j}
j}  be algebraic over F,
be algebraic over F,  ,X)).
,X)). )/F) = n.
(2). {1,
)/F) = n.
(2). {1, ,
, 2,...,
2,..., n-1} is a basis for F(
n-1} is a basis for F( ) over F.
The subfield
) over F.
The subfield  1,...,
1,..., n)
n)| Back | Table of Contents |
|
|
Examples of Splitting FieldsLet us now give some examples of splitting fields. Throughout this section let F be a field, Example 1: the zeros of f in C are given by the quadratic formula
(-a +
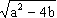 )/2, (-a - )/2, (-a - 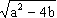 )/2, )/2,
where
Ef = Q(
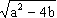 ). ).Let us analyze the situation further: We consider two cases. Case 1: f is reducible in Q[X]. In this case, the zeros of f are contained in Q and Case 2: f is irreducible in Q[X]. Note that by (1), Ef can be obtained from Q by adjoining either one of those zeros of f. Therefore, by Theorem 3 of the section on algebraic numbers,
deg(Ef /Q) = deg(f ) = 2.
Example 2: The zeros of f in C are just the nth roots of 1. Let
1,
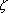 , ,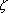 2,..., 2,...,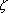 n-1. n-1.
Since all these roots are contained in
Ef = Q(
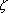 ). ).The field Ef is called the nth cyclotomic field. The term "cyclotomic" means "circle dividing" and the reason for this terminology is that the field Ef was first considered in connection with the problem of constructing a regular polygon of n sides using only a ruler and compass. Let us determine the degree of Set (3) n(X) = n(X) = 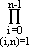 (X - (X - 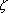 i ). i ).Then
Xn - 1 =
(4)
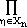 (X - (X - 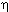 ) )
=

=
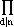  d(X). d(X).
Let us use formula (4) to compute  1(X) = X - 1. 1(X) = X - 1.
For  1(X) · 1(X) ·  2(X) = X2 - 1. 2(X) = X2 - 1.Therefore, by (5), (6) 2(X) = X + 1. 2(X) = X + 1.
For
X3 - 1 =
 1 · 1 ·  3(X), 3(X),and thus by (5), (7) 3(X) = (X3 - 1)/(X - 1) = X2 + X + 1 3(X) = (X3 - 1)/(X - 1) = X2 + X + 1
For
X4 - 1 =
 1(X) · 1(X) ·  2(X) · 2(X) ·  4(X), 4(X),and thus by (5) and (6),  4(X) = (X4 - 1)/[(X - 1)(X + 1)] 4(X) = (X4 - 1)/[(X - 1)(X + 1)]
= X2 + 1.
From these few computation, it becomes clear that if we have computed  n(X) = (Xn - 1)/ n(X) = (Xn - 1)/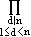  d(X). d(X).
We observe that
A more careful analysis of the algorithm for computing
= deg(
 n(X)) n(X))
=
 (n), (n),
where
Theorem 1: If Example 3: Let 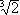 , , 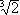 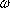 , , 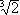 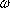 2, 2,
where
Since
Moreover, Thus, by Theorem 3 in the section on algebraic extensions, (13)
< 2 · 3 = 6
Note, however, that But by Theorem 3 of algebraic extensions and (14), (15)Similarly, (16)by (15). By (15) and (16), we see that (17)Finally, by (13) and (17), (18)Example 4: Let Let a1/n be any nth root of a in C and let
a1/n, a1/n
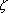 , a1/n , a1/n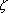 2, ..., a1/n 2, ..., a1/n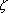 n-1. n-1.Thus,
= Q(a1/n,
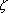 ). ).Calculating the degree of Ef over Q is a rather intricate problem, and we will not consider a complete solution at this time. However, let us say what we can without undue expenditure of effort. Note that and (19)
by Theorem 1. Therefore, in order to compute
Since and therefore,
< deg(Xn - a)
= n.
Thus, finally, by (19) we see that (20)
In special cases, we can compute
Theorem 2: Let p be prime and suppose that
deg(Ef /Q) = p(p - 1).
Proof: Since p is prime, we have (21) (p) = p - 1, (p) = p - 1,
(p - 1, p) = 1.
By equations (19) and (21), Therefore, since
= p · deg(Ef /Q(a1/p)),
we see that
p|deg(Ef /Q).
Thus, by (22), we have Example 5: Let F be a subfield of C which contains the nth roots of 1 for some
a1/n, a1/n
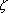 , ..., a1/n , ..., a1/n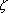 n-1, n-1,
where
Ef = F(a1/n, a1/n
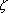 , ..., a1/n , ..., a1/n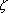 n-1) n-1)
= F(a1/n).
The extension |
| Back | Table of Contents |