
 C be constructible. Then there exists a set of complex numbers {
C be constructible. Then there exists a set of complex numbers { 1,...,
1,..., n} such that
n} such that  12
12  Q,
Q, i2
i2  Q(
Q( 1,...,
1,..., i-1)
i-1)
 Q(
Q( 1,...,
1,..., n).
n). is constructible,
is constructible,  )/Q) = 2k
)/Q) = 2k
 C be constructible. Then there exists a set of complex numbers {
C be constructible. Then there exists a set of complex numbers { 1,...,
1,..., n} such that
n} such that  12
12  Q,
Q, i2
i2  Q(
Q( 1,...,
1,..., i-1)
i-1)
 Q(
Q( 1,...,
1,..., n).
n). is constructible,
is constructible,  )/Q) = 2k
)/Q) = 2k ·v
·v
 F
F E
E and v, considered as elements of E. The dimension of E over F is called the degree of E over F, denoted
and v, considered as elements of E. The dimension of E over F is called the degree of E over F, denoted | Back | Table of Contents |
|
|
Constructions with Straightedge and CompassWe may not appear to have accomplished anything of significance yet concerning the theory of fields, but we have enough machinery to apply to several significant problems. In this section we will consider the problem of constructing geometrical figures using only a compass and a straightedge. For our purposes, a straightedge is a device which can be used only to draw a line between two points and a plane. It has no measurement capabilities. Such constructions were first considered by the Greek geometers and are probably familiar to the reader from a high school course in geometry. The Greeks posed three very interesting questions concerning constructibility which they were unable to solve:
Problem 1: (Trisecting an Angle) Given an arbitrary angle Problem 2: (Duplicating a Cube) Given an arbitrary cube C of volume V, construct a cube having volume 2V, using only straightedge and compass. Problem 3: (Squaring a Circle) Given an arbitrary circle C of area A, construct a square having area A, using only straightedge and compass. Our plan in this section is to first discuss the general problem of constructibility. From this discussion will emerge a powerful theory which will provide immediate solutions to Problems 1 and 2 and will point the way to a solution of Problem 3. It will turn out that all three problems have no solution. We will turn our attention to the construction of regular polygons. Let us first lay down the ground rules for our investigation. Let us restrict ourselves to plane constructions. Further, we will identify the Euclidean plane with the complex numbers, by identifying the point with coordinates Let us now reduce our geometric problem to an algebraic problem. It is clear that each geometric figure which we can construct can be defined by a finite number of points, line segments, and circular arcs. Let us describe a given geometrical figure by means of a family of complex numbers as follows: The finite number of points can be viewed as complex numbers as described above. A line segment is described by the complex numbers corresponding to its endpoints. A circular arc is described by four numbers: two corresponding to the endpoints of the arc, on corresponding to the center of the circle, and one equal to the length of the radius of the circle. It is clear that the numbers described are necessary and sufficient to construct the geometrical figure. Thus, let us henceforth think of a geometrical figure in terms of a collection of complex numbers describing points, lines and arcs in the figure. It is clear that in order to construct a given figure, it is both necessary and sufficient to be able to construct the line segments connecting
Definition 1: A complex number From our above discussion we have Theorem 2: A geometrical figure is constructible if and only if each of the complex numbers describing it is constructible. Thus, our original question concerning constructibility of geometric figures is reduced to one concerning constructibility of complex numbers. Let C denote the set of all constructible complex numbers. We will give a more-or-less complete description of C. Before proceeding further, let us recall some of the possible elementary constructions of Euclidean geometry. For the actual constructions refer back to high school geometry. Basic Constructions 1. Bisect a given angle. 2. Construct a line perpendicular to a given line segment L at a given point P on L. 3. Construct a line through a given point P which is parallel to a given line L. 4. Given line segments of lengths l and l', construct a line segment of length ll'. 5. Given a line segment of length l, construct a line segment of length 1/l. 6. Given a line segment of length l, construct a line segment of length 7. Construct an angle equal to the sum of two given angles. Examples of some of these constructions are given in theappendices. Theorem 3: C is a subfield of C. Proof: Our assertion amounts to the following: If 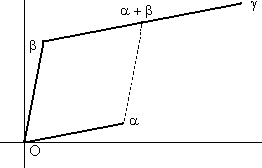
Figure 1: Construction of  + +  . .
In order to construct - 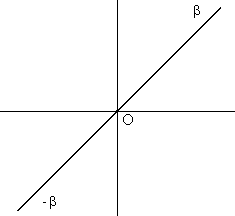
Figure 2: Construction of -
 Let us construct  = r1(cos = r1(cos 1 + i sin 1 + i sin 1). 1). = r2(cos = r2(cos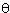 2 + i sin 2 + i sin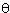 2). 2).By de Moivre's theorem,  · ·  = r1r2[cos( = r1r2[cos(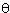 1 + 1 + 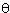 2) + i sin( 2) + i sin(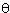 1 + 1 + 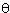 2)] 2)]
Thus, the line segment O 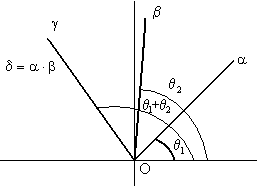
Figure 3: Construction of
 · ·  Finally, assume that
1/
 = r2-1(cos = r2-1(cos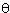 2 + i sin 2 + i sin 2)-1 2)-1
= r2-1[(cos
 2 - i sin 2 - i sin 2)/(cos2 2)/(cos2 2 + sin2 2 + sin2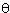 2)] 2)]
= r2-1[cos(-
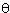 2) + i sin(- 2) + i sin(-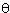 2)]. 2)].
Thus, the line segment O Corollary 4: All rational numbers are constructible. Proof: We have bee given 1 as part as our initial data. Thus,
Proposition 5: Let Proof: Without loss of generality, assume that 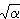 = ± = ± 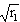 [cos( [cos( 1/2) + i sin( 1/2) + i sin( 1/2)]. 1/2)].
Let us only consider the positive sign. The reasoning for the negative sign is similar. Then the line segment O
Theorem 6: Let
Proof: By Corollary 4, every element of Q is constructible and by Proposition 5 and the assumption The amazing fact is that the converse is also true. We have
Theorem 7: Let
and such that Before proceeding with the proof of Theorem 7, let us do some preliminary work. Assume that the points We will consider separately three cases: Case 1: The lines L1 and L2 have equations
L1: a1x + b1y + c1 = 0,
(3)
L2: a2x + b2y + c2 = 0,
where  m m  Fm-1, Fm-1,  m m  Fm-1 Fm-1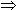 Fm = Fm-1 Fm = Fm-1
since Case 2: The line L and the circle C have the equations
L: ax + by + c = 0,
(5)
C: dx2 + ey2 + fx + gy + h = 0,
where
Fm
 Fm-1( Fm-1(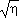 ), ),
since Case 3: The equations of C1 and C2 are given by
C1: x2 + y2 + a1x + b1y + c1 = 0,
C2: x2 + y2 + a2x + b2y + c2 = 0,
where
(a1 - a2)x + (b1 - b2)y + (c1 - c2) = 0.
Therefore, by case 2, there exists
Fm
 Fm-1( Fm-1(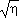 ). ).By comparing the results of cases 1-3, we have
Lemma 8: Suppose that the points
Then there exists Proof: By (6) and (7) we are done in cases 2 and 3. In case 1 we may set Let us now prove Theorem 7. Suppose that
Fm
 Fm-1( Fm-1( ). (1 < m < n). ). (1 < m < n).Define  0 = i, 0 = i,  j = j = 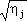 (1 < j < n). (1 < j < n).We assert that (9)
This follows trivially by induction from (8). It is clearly true for
Fm
 Fm-1( Fm-1( m) m)
This completes the induction and hence (9) is proved. It is clear that
Finally, by (9) for
This completes the proof of the first assertion of Theorem 7. In order to show that
for some r. But, if we set
= 2r
for some r. Let us now illustrate Theorem 7 by applying it to the problem of trisecting an angle. Not only will we show that there is no general procedure for trisecting an angle with compass and straightedge, but there are particular angles which cannot be trisected, For example, let us prove: Theorem 9: A 60o angle cannot be trisected using only a compass and a straightedge. Proof: It is well known that a 60o angle can be constructed using only a compass and a straightedge. Therefore, a 60o angle can be trisected if and only if it is possible to construct a 20o angle using only a compass and a straightedge. But let us see what it means for an angle
cos(20o) + i sin(20o) =
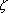 is constructible. 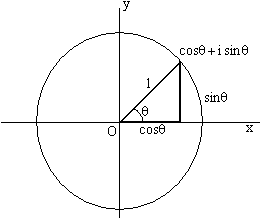
Figure 4: Construction of the Angle
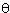 . .Let us assume that
= 6.
Thus, a contradiction is reached and Let us next turn to the problem of duplicating the cube. For simplicity's sake let us consider a cube C of side 1. We wish to construct a cube of volume 2. This is equivalent to constructing a line segment of length
Therefore, by Theorem 7, we see that Theorem 10: It is impossible to duplicate the cube of side 1 using only a straightedge and compass. Let us now turn to the problem of squaring the circle. For the sake of simplicity, let us consider the circle of radius 1. It has area equal to Let us now take up the problem of the construction of a regular polygon of n sides. Constructing such a polygon is equivalent to constructing such a polygon is equivalent to constructing an angle of 360/n. But as we saw in the proof of Theorem 9, the angle
cos(360/n) + i sin(360/n) =
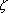 n n
is constructible. But
Table 1: Values of
 (n) (n)
Let
n = p1r1· p2r2··· ptrt (ri > 0)
be the decomposition of n into a product of powers of distinct primes p1,..., pt. Then (10) (n) = (n) =  (p1r1) ··· (p1r1) ···  (ptrt), (ptrt),
so that  (pjrj) = pjrj-1(pj - 1). (pjrj) = pjrj-1(pj - 1).
Therefore, if
p = 2k + 1
= 2qu + 1
= (2u + 1)(2(q-1)u - 2(q-2)u + .. + 1),
which contradicts the fact that p is prime. Thus, we have shown that if
22v + 1
is called a Fermat prime. The first few Fermat primes after 3 are
221 + 1 = 5,
222 + 1 = 17,
223 + 1 = 257,
224 + 1 = 65,537.
It is not true that every integer of the form Theorem 11: In order for a regular polygon of n sides to be constructible using only straightedge and compass, it is necessary and sufficient for n to be of the form
n = 2rp1p2...pw,
where p1p2...pw are distinct Fermat primes. |
| Back | Table of Contents |