M is a maximal ideal of R if and only if R/M is a field. Let f1(X), f2(X),..., fr(X), be monic polynomials belonging to F[X] such that deg f(X) > 1 (1 < i < r). Then there exists an extension E of F such that in E[X], each polynomial f1(X) splits into a product of linear factors. Let R be a ring. An ideal of R is a subring I of R such that if a element of I, r element of R, then a · r element of I and r · a element of I. An ideal A of R is said to be proper if Anot equalR. An ideal M of R is said to be a maximal ideal if (a) M is a proper ideal and (b) if A is a proper ideal containing M, then M = A. If alpha1,...,alphan are algebraic over F, then F(alpha1,...,alphan) is of finite degree over F and is therefore algebraic over F. Let F be a field. Then there exists an algebraically closed extension E of F. Let alpha and beta be algebraic over F, then alpha ± beta, alpha · beta, alpha/beta (beta not equal 0) are algebraic over F. Let E/F be finite. Then E is algebraic over F. Let alpha element of E be algebraic over F. alpha the zero of a monic irreducible polynomial p element F[X]. The polynomial p is called the irreducible polynomial of alpha over F denoted IrrF(alpha,X) Let E subset of F subset of G be three fields. Assume that deg(F/E) and deg(G/F) are finite. Then deg(G/E) is finite and deg(G/E) = deg(G/F) · deg(F/E). Further, if {alpha1,...,alphan} is a basis of G over F and {beta1,...,betam} is a basis of F over E, then {alphaibetaj} (1 < i < n, 1 < j < m) is a basis for G over E. Let alpha be algebraic over F, n = deg(IrrF(alpha,X)). Then - (1) deg(F(alpha)/F) = n. and (2) {1,alpha,alpha2,...,alphan-1} is a basis for F(alpha) over F. A field F is said to be algebraically closed if every nonconstant polynomial in F[X] splits into a product of linear factors in F[X]. We say that alpha is algebraic over F if there exists a nonzero polynomial f element of F[X] such that f(alpha) = 0. If alpha is not algebraic over F, then we say that alpha is transcendental over F. Let F be a field and let E be an extension of F. We say that E is an algebraic extension of F if every alpha element of E is algebraic over F. If f has a leading coefficient 1, then we say that f is monic. The set of rational numbers. The complex numbers.
Back | Table of Contents

Algebraically Closed Fields

In the beginning of the nineteenth century, Gauss proved the following remarkable property of the field C of complex numbers:

Theorem 1: Let f(X) element of C[X] be nonconstant. Then, in C[X], f(X) splits into a product of linear polynomials.

This fact, while not surprising to a student who has spent some time trying to solve polynomial equations, is rather deep. One of the shortest proofs of Gauss's theorem relies on complex analysis and uses Liouville's theorem to the effect that a bounded, entire function is constant. Elsewhere, we will give a proof, due to Artin, which is almost purely algebraic in character, and which uses Galois theory. Artin's proof makes use of the fact that every polynomial of odd degree and having real coefficients has a real zero. However, for the rest of this section, let us assume Gauss's theorem. This will not result in any circular reasoning since we will use the theorem only for purposes of illustration.

Gauss's theorem asserts that the field of complex numbers has a rather special property which we now formalize in a definition:

Definition 2: A field F is said to be algebraically closed if every nonconstant polynomial in F[X] splits into a product of linear factors in F[X].

Example 1: According to Gauss's theorem C is algebraically closed.

Example 2: Let

Q = {alpha element of C | alpha is algebraic over Q}.

We will prove that Q is algebraically closed .

Proposition 3: The following statements are equivalent:

(1) F is algebraically closed.

(2) If E is an algebraic extension of F, then E = F.

Proof: (1) implies (2). Let E be an algebraic extension of F and let alpha element of E. Then alpha is algebraic over F. Moreover, if f = IrrF(alpha,X) is a nonconstant, monic polynomial in F[X]. Therefore, since F is algebraically closed,

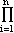f = product over i(X - alphai),   alphai element of F.

But alpha element of E is a zero of f, so that X - alpha divides f (in E[X]). Therefore, X - alpha = X - alphai for some i, and thus alpha = alphai for some i, so that alpha element of F. Therefore, E subset of F. But by assumption, E superset of F, so we have proved E = F.

(2) implies (1). Let f be a nonconstant polynomial in F[X]. We must show that f splits into a product of linear factors in F[X]. Without loss of generality, we may restrict ourselves to the case of f monic and irreducible in F[X]. In this special case, we will prove that deg(f ) = 1 so that f is linear. Let n = deg(f ). By adjoining a root alpha of f to F, we get an extension F(alpha) of F of degree n (Theorem 3 of the section on algebraic numbers). But by Proposition 1 of the section on Algebraic extensions, F(alpha) is an algebraic extension of F. Therefore, by our hypothesis (2), F(alpha) = F, so that n = deg(F(alpha)/F) = 1. Thus, f is linear.

In the section on splitting fields, we showed that it is possible to construct an extension E of a given field F in which any given finite collection of nonconstant polynomials in F[X] splits into linear factors. At this point we would like to strengthen this result by proving that F is contained in an algebraically closed field. This result will prove to be of great utility to us in studying the properties of F, since we can fix, once and for all, an extension of F, which is so large as to accommodate the roots of all polynomial equations over F within it. Our main result is

Theorem 4: Let F be a field. Then there exists an algebraically closed extension E of F.

The proof of Theorem 4 is rather difficult and will be delayed momentarily. It is probably best for the beginner to omit the proof of Theorem 4 entirely and concentrate effort on understanding the many significant ramifications it has.

If F is a field and E is an algebraically closed field containing E, then E will usually be "too big." For example, E will usually contain elements which are transcendental over F. Since it is convenient to work only with algebraic elements, let us make the following definition.

Definition 5: An algebraic closure of a field F is an extension F of F such that (1) F is algebraically closed, and (2) F is an algebraic extension of F.

The main result of this section is

Theorem 6: Let F be a field. Then F has an algebraic closure.

Proof: Let E be an algebraically closed extension of F. E exists by Theorem 4. Set

F = {alpha element of E | alpha is algebraic over F}.

We assert that F is an algebraic closure of F. By Corollary 6 of the section on algebraic extensions, F is a field. It is clear that F is an algebraic extension of F. So we must show that F is algebraically closed. Let f element of F[X], deg(f ) > 1. In order to show that F is algebraically closed, we must show that f splits into a product of linear factors in F[X]. Without loss of generality, assume that f is monic. Since E is algebraically closed,

(1)
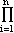f = product over i(X - alphai),   alphai element of E.

Let f = Xn + a1Xn-1 + ... + an, ai element of F. Then alphai is algebraic over F(a1,...,an) which implies that

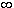
deg(F(alphai,a1,...,an)/F(a1,...,an)) < infinity

by Theorem 3 of algebraic extensions. But aj element of F (1 < j < n) implies aj is algebraic over F implies F(a1,...,an) is of finite degree over F (Corollary 5 of algebraic extensions). Therefore, by Theorem 3 of algebraic extensions

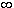deg(F(alphai,a1,...,an)/F) < infinity
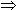impliesalphai is algebraic over F (Proposition 1 of algebraic extensions)
implies alphai element of F.

Therefore, by (1), f splits into linear factors in F[X].

Example 3: C is an algebraic closure of R.

Example 4: Let

Q = {alpha element of C | alpha is algebraic over Q}.

Then, by the proof of Theorem 6, Q is an algebraic closure of Q. The field Q is called the field of algebraic numbers.

Note: Q not equal C. For example, pi element of C - Q by Lindemann's theorem.

We shall now turn our attention to the proof of Theorem 4. The principal difficulty in the proof is to pass from the finite collections of polynomials to (possibly) infinite ones. This is usually accomplished via Zorn's lemma. Indeed the present proof, which is due to Artin, makes use of Zorn's lemma, but in a rather disguised form. We use the fact that if I is a proper ideal of a commutative ring R with unity, then I is contained in a maximal ideal. And it is this fact which requires Zorn's lemma.

The bulk of Theorem 4 resides in the following lemma.

Lemma 7: Let K be a field. Then there exists an extension PK of K such that every nonconstant polynomial f element of K[X] has a zero in PK.

Proof: Let

A = {f element of K[X] | f is nonconstant and irreducible}.

For each f element of A, let Yf denote an indeterminate. Let us consider the ring R = K[Yf]f element of A, gotten by adjoining to K all the indeterminates Yf. A typical element of R is a polynomial in finitely many indeterminates Yf, having coefficients in K. Let I denote the ideal of R generated by the polynomials

f(Yf )    (f element of A).

We assert that I not equal R. For if I = R, then 1 element of I, so that

(2)
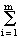1 = sum over i to mgi f(Yf ),    gi element of R,

where we may assume, without loss of generality, that

gi = gi(Yf1,...,Yfm).

By Corollary 6 of the section on splitting fields, there exists an extension E of K in which each of the polynomials fi has a zero alphai (1 < i < m). The relation (2) only involves polynomials in K[Yf1,...,Yfm]. Let us replace Yfi in (2) by alphai. Then, since alphai is a zero of fi, equation (2) yields 1 = 0, a contradiction. Therefore, Inot equalR. Thus, I is contained in a maximal ideal M of R. Now R/M is a field by Theorem 8 if the section on maximal ideals. Moreover, the mapping

xmaps tox + M   (x element of K)

is an isomorphism of K into R/M. Let us identify K with its image in R/M. Then R/M becomes a field extension of K. Set Pk = R/M. Let f element of K[X] be nonconstant and irreducible. Then

f(Yf + M) = f(Yf ) + M = 0 + M

since f(Yf ) element of M. Therefore, Yf + M is a zero of f in R/M. We have therefore shown that every irreducible, nonconstant polynomial in K[X] has a zero in PK, which completes the proof of Lemma 7.

Proof of Theorem 4: Let us construct a sequence of fields

E0 subset of E1 subset of E2 subset of ...

as follows: Set E0 = F and for i > 0, set

Ei+1 = PEi,

where PEi is the field described in the lemma. Let

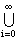E = union over infinityEi.

If alpha,beta element of E then for all sufficiently large i, alpha,beta element of Ei. Therefore, alpha ± beta, alpha · beta alpha/beta (betanot equal0) are defined as elements of Ei for all i sufficiently large and are independent of the choice of i. Thus we can define the field operations on E and E becomes a field. We contend that E is algebraically closed. For let f element of E[X], n = deg(f ) > 1. We must show that f splits into a product of linear factors in E[X]. This assertion is trivial for n = 1. Let us proceed by induction on n. Assume that n > 1 and assume the assertion for polynomials of degree < n. Since f element of E[X], f element ofEi[X] for some i. Therefore, by construction of Ei, f has a zero alpha in Ei+1, so that f = (X - alpha)g in Ei+1[X], where deg(g) > 1. Therefore, f = (X - alpha)g in E[X], where 1 < deg(g) < n. Therefore, by induction, g is a product if linear factors in E[X], so that f is a product of linear factors in E[X].
Back | Table of Contents